
|
|
|||||||
| مقالات و موضوعات علمی در این تالار مقالات و مطالب علمی قرار داده خواهد شد توجه شود که مقالات علمی و دانشگاهی با اخبار علمی تفاوت دارد و بخش مربوطه ی اخبار علمی به صورت جداگانه ایجاد شده است |
 |
|
|
ابزارهای موضوع | نحوه نمایش |
|
#1
|
||||
|
||||
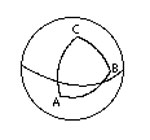 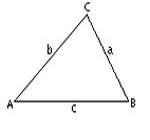 مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلث
یکی از مهمترین قضایای موجود در مثلثات قضیه فیثاغورث میباشد.در این قضیه رابطه بین وتر و اضلاع قائم یک مثلث قائم الزاویه بیان میشود. محاسبه مساحت مثلث برای محاسبه مساحت یک مثلث روشهای مختلفی وجود داردو در ادامه به توضیح این روشها میپردازیم روش هندسی برای محاسبه مساحت یک مثلث باید طول ارتفاع مثلث و نیز طول قاعده(ضلعی که ارتفاع بر آن عمود است) آن را داشته باشیم.آنگاه میتوانیم از فرمول زیر استفاده کنیم: 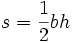 در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است: 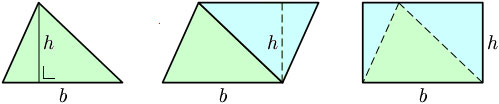 برای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود.
__________________
|
| جای تبلیغات شما اینجا خالیست با ما تماس بگیرید | |
|
|
|
|
#2
|
||||
|
||||
|
روش برداری
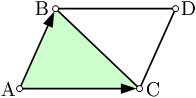 از ضرب خارجی دو بردار مساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| خواهد بود.این مفدار ،اندازه ضرب خارجی دو بردار AB و AC میباشد.پس مساحت مثلث ABC برابر با نصف اندازه ضرب خارجی دو بردار AB و AC خواهد شد. روش مثلثاتی 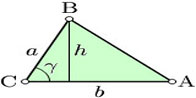 برای پیدا کردن ارتفاع مثلث ارتفاع یک مثلث را میتوان با استفاده از روابط مثلثاتی بدست آورد.به عنوان مثال در شکل روبرو ارتفاع مثلث از فرمول  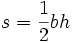 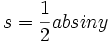 روش مختصاتی فرض میکنیم نقطه A به مختصات (0, 0)یک راس از مثلث باشد و نقاط B به مختصات(x1, y1) و C به مختصات(x2, y2) دو راس دیگر مثلث باشند.در این صورت مساحت مثلث نصف مقدار|x1y2 − x2y1| خواهد شد. فرمول heron راه دیگر محاسبه مساحت مثلث استفاده از فرمول heron است. این فرمول به صورت زیر است: 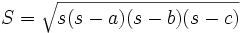
__________________
|
|
#3
|
||||
|
||||
|
کاربرد مثلث در موسیقی
 اهرام مصر مثلث از ابتدایی ترین اشکال هندسی بوده که انسانها در هنر ازاون استفاده میکردند، بدون شک اولین نوع از انواع مثلث هم که در هنر از آن استفاده شده مثلث متساول الاضلاع بوده است. اهرام مصر نمونه بسیاری قدیمی (حدود 2800 سال پیش از میلاد) از کاربری مثلت در هنر معماری قدیم بوده است. نمونه های دیگر از استفاده از مثلث در هنر تمدن های قدیم را می تواند در کاشی کاری های دیواره معابد Pompeii در نپال نیز مشاهده کرد. معروف هست تالس (640-550 سال پیش از میلاد) که پدر ریاضیات، نجوم و فلسفه یونان باستان بوده از شاگردان خود می خواهد که به مصر سفر کنند تا از پیشرفت علوم در آن تمدن اطلاعات لازم را کسب کنند و فیثاغورث (Pythagoras) از اولین افرادی بوده که این دستور را می پذیرد و به مصر سفر میکند. فیثاغورث از بنیانگذاران علمی موسیقی در جهان بوده و اغلب از هندسه برای مدل کردن استفاده می کرده، می خواهیم با استفاده از تجربیات او سلسه مطالبی را پیرامون ارتباط موسیقی با علوم هندسه، فیزیک و ریاضی آغاز کنیم. 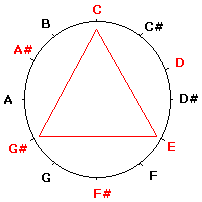 مثلث متساول الاضلاع معادل یک آکورد افزوده موسیقی را می توانیم به روشهای مختلف مدل کنیم برای شروع کار ساده ترین روش را انتخاب میکنم که عبارت است از مدل کردن عمودی موسیقی یاهمان هارمونی. این روش مدل کردن به موسیقیدان ها کمک می کند تا هنگام فکر یا گوش کردن به هارمونی تصویر بهتری از نت های موسیقی داشته باشند بخصوص برای نوازندگان سازغیر از پیانو. یک دایره در نظر بگیرید و آنرا به دوازده قسمت مساوی (یک اکتاو کروماتیک) تقسیم کنید و نت ها را به ترتیب روی هر قسمت بنویسد مانند شکل. یکی از ساده ترین اشکال هندسی که در این دایره تقسیم شده می توان ساخت مثلت متساوی الاضلاع می باشد. که اگر آنرا بسازید و به آن دقت کنید تفسیر موسیقی آن یک آکورد افزوده خواهد بود. حتما" شنید که آکوردهای افزوده جدای از اینکه معکوس باشند یا نه چهار حالت بیشتر نیستند که دایره فوق این موضوع را بسادگی نمایش میدهد چرا که اگر راس بالایی مثلث را در جهت عقربه های ساعت حرکت دهیم تا رسیدن به نت E و انطباق دوباره روی خود، می تواند سه حالت دیگر را به خود بگیرد. همچنین به وضوح در شکل می توان دید که یک آکورد افزوده از سه فاصله (که در اینجا هرکدام یک ضلع مثلث هستند) یکسان معادل 4 نیم پرده تشکیل شده است. 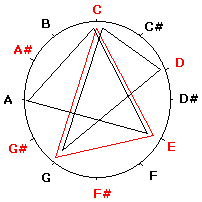 آکوردهای بزرگ، کوچک، sus2 و sus4 شما باز هم می توانید مثلث های دیگری درست کنید. به شکل بعدی نگاه کنید که آکوردهای دو ماژور و لا مینور را نمایش میدهد. این دو مثلث (آکورد) خصوصیات جالبی دارند اولا" اضلاع آنها باهم برابر است، ثانیا" نسبت به خطی که از D کشیده میشود و به G# خطم میشود متقارن می باشند، حتما" می دانید که مینور نسبی گام دو ماژور، لامینور می باشد. به این طریق شما می توانید یک روش ساده برای پیدا کردن گامهای مینور و ماژور نسبی پیدا کنید، هر چند اینکار در پیانو بخاطر وضوح دیداری که چیدمان نت ها وجود دارد ساده می باشد. مثلث های متساوی الساقین هم جالب هستند یکی از آنها آکورد sus2 را تشکیل میدهد که در شکل مشاهده میکنید و همچنین میتوانید آکوردهای کاسته را نیز باز با یک مثلث متساوی الساقین درست کنید. اگر دقت کنید این مثلث متساوی الساقین حالت آکورد sus2 برای C و حالت آکورد sus4 برای G دارد. بنابراین می توان به ارتباط نزدیک آکوردهای sus در حالت های 2 و 4 برای فاصله های پنجم با یکدیگر پی برد. این نکته هم جالب خواهد بود اگر شما راس D در این مثلث را نسبت به راس C قرینه کنید به آکورد sus2 دیگری می رسید که یک پرده عقب تر است آکورد Csus4 قرار دارد. شما می توانید دامنه مدل کردن را ادامه دهید و راجع به سایر مثلث ها فکر کنید، همچنین می توانید آکوردهای چهار صدایی را با انواع چهار ضلعی ها مدل کنید. سئوالی که پیش می آید این است که آیا هستند افرادی که با شنیدن موسیقی این اشکال در ذهن آنها نقش ببندد؟
__________________
|
|
#4
|
||||
|
||||
|
مثلث قائمالزاویه مثلثی است که یکی از زوایای آن قائمه (۹۰ درجه) باشد
در حالت خاص اگر یکی از زوایا ۳۰ درجه باشد، ضلع مقابل آن زاویه نصف وتر است.وتر به ضلع روبرو به زاویه 90 درجه میگویند* بزرگترین ضلع در مثلث قائم الزاویه وتر است در مثلث قائمالزاویه مجموع مربعهای طول دو ضلع برابر با مربع طول وتر است. برابرنهاده فرهنگستان زبان فارسی دوره پیش از انقلاب برای واژه قائمالزاويه، «راستگوشه» بود که چندی هم در کتابهای درسی بکار رفت.
__________________
|
|
#5
|
||||
|
||||
|
3، 6، 10، 15، 21 و ... بنظر شما این اعداد چه ویژگی مشترکی دارند؟ اگر دست بهقلم نشویم و شکل نکشیم و آزمایش نکنیم، فهمیدن ارتباط میان آنها کمی دشوار است. بهاین شکل دقت کنید مشکل شما حل خواهد شد. به اعداد موجود در این سری، اعداد مثلثی میگوییم.
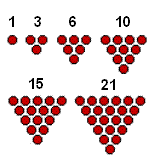 1 = 1 3= 1+2 6= 1+2+3 10= 1+2+3+4 15= 1+2+3+4+5 21= 1+2+3+4+5+6 . . . اما شکل اول یک ایده جدید به ما می دهد کهمی توانیم این اعداد را همانند پاراگراف بالا نیز تفسیر کنیم. به بیان دیگرمی توان گفت که هرعدد مثلثی تشکیل شده است از حاصل جمع یکسری از اعداد متوالیطبیعی. به این معنی که اولین عدد مثلثی مساوی است با مجموع یک عدد از اعداد طبيعي، دومین معادل است با مجموع دو عدد از اعداد طبیعی، سومین معادل است بامجموع سه عدد از اعداد طبیعی و ... و بالاخره n امین عدد مثلثی معادل است با مجموعn عدد از اعداد طبیعی که اگر رياضياتدبیرستان را هنوز فراموش نکرده باشید بخاطر خواهید آورد که مقدار این عدد معادلn(n+1)/2 خواهد بود. (یک تصاعد حسابيساده(  مجموع دو عدد مثلثی متوالی اگرهر دو عدد پشت سرهم در سری اعداد مثلثی را با هم جمع کنیم حاصل جمع یک عددمربعمی شود. مثلا" 1+3=4 یا 3+6=9 یا6+10=16 و ... البته دلیل آن ساده است به شکل دوم توجه کنید و ببینید که چگونه دو مثلثقرمز و سبز روی همتشکیل یک مربع را می دهند. (سعی کنید با استدلال ریاضی هم این موضوع را ثابت کنید،ساده است از همان رابطه بالا استفاده کنید.) مطلب اخیر اغلب بصورت قضیه مربع هر عدد طبیعی برابر است با مجموع دو عدد مثلثی متوالینیز مطرح می شود.
__________________
|
|
#6
|
||||
|
||||
|
شکلهای مسطح را هم نهشت گویند اگر همریخت و هم اندازه باشند. شکلهای همنهشت را میتوان با تبدیلی که نقاط را حرکت میدهد ، اما رابطه های برخوردی "incidence" (بین نقاط و خطوط)، زوایای بین خطوط، و طولهای پاره خطها را تغییر نمی دهد، بر هم منطبق کرد.
چنین تبدیلی سطحها را حفظ میکند و خطوط موازی را موازی جابجا میکند. اگر شکلهای همنهشت دارای جهت یکسان ( نسبت به جهت ثابتی از صفحه) باشند، آنها را میتوان با استفاده از دنباله ای از انتقالها و دوران های صفحه به هم تبدیل کرد. چنین شکلهایی را مستقیم-هم نهشت " directly congruent" می نامند. اگر دارای جهت یکسان نباشند آنگاه برای منطبق کردن یکی بر دیگری، میتوان دنباله ای را بدست آورد که غیر از انتقالها و دوران های متوالی حاوی تقارنی منفرد نسبت به خطی راست باشد. شکلهایی چنین را وارون - همنهشت "inversely congruent" می نامند. انتقالها ، دورانها و تقارنها به تبدیل های هم نهشتی موسوم اند و می توانند در بررسی شکلهای مسطح به عنوان معیارهای همنهشتی به کار روند، اما این کاربرد به هیچ وجه در برگیرنده سودمندی آنها به عنوان وسیله ای در کشف مطالب تازه هندسی نیست.
__________________
|
|
#7
|
||||
|
||||
|
چهار قضیه در مورد همنهشتی مثلثها
در تعریف همنهشتی نیاز است که شکلها در جمیع جنبه ها سازگار باشند، بخصوص طولهای اضلاع متناظر و زوایای بین انها برابر باشند. قضایای زیر بیان میکند که در مورد حالات خاصی از مثلثها کافی است که برای امتحان هم نهشتی سه جز آنها را مورد بررسی قرار دهیم. اگر این سه جز در دو مثلث برابر باشند مثلثها همنهشت هستند. چهار قضیه همنهشتی 1. دو مثلث هم نهشت اند اگر طول یک ضلع یکی از انها برابر طول ضلع نظیرش از دیگری و دو زاویه آنها برابر دو زاویه نظیرشان از دیگری باشد 2.دو مثلث هم نهشت اند اگر طولهای دو ضلع یکی برابر طولهای ضلعهای نظیرشان از دیگری و زاویه های بین این ضلعها برابر باشند 3.دو مثلث هم نهشت اند اگر طولهای دو ضلع یکی برابر طولهای ضلعهای نظیرشان از دیگری و زاویه های مقابل ضلع های بزرگتر آنها برابر باشند 4. دو مثلث هم نهشت اند اگر طولهای سه ضلع از یکی برابر طولهای ضلعهای نظیرشان از دیگری باشند. اشکال چهار قضیه 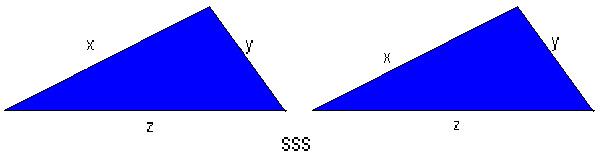  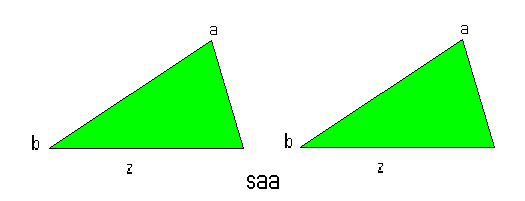 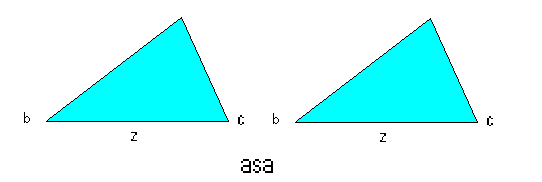
__________________
|
|
#8
|
||||
|
||||
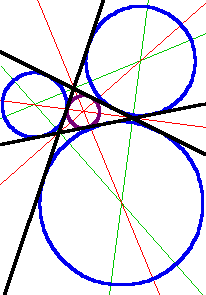 با دایره داخلی (بنفش)، دوایر خارجی (آبی)، نیمسازهای زوایای داخلی (قرمز) و نیمسازهای زوایای خارجی (سبز) دایره های محاطی داخلی و خارجی یک مثلث در هندسه، دایره محاطی داخلی یک مثلث بزرگترین دایرهای است که آن مثلث میتواند در بر بگیرد؛ این دایره سه ضلع آنرا لمس مینماید ( بر آنها مماس میباشد). مرکز دایره محاطی مرکز داخلی مثلث نامیده میشود. یک دایره محاطی خارجی مثلث، یک دایره در خارج مثلث است که بر یکی از اضلاع مثلث و امتداد دو ضلع دیگر مماس باشد. هر مثلث دارای سه دایره محاطی خارجی متمایز، که هر کدام بر یکی از اضلاع مثلث مماس میباشد. مرکز دایره محاطی داخلی بر روی تقاطع نیمسازهای زوایای داخلی قرار دارد. مرکز یک دایره محاطی خارجی بر روی تقاطع نیمساز یک زاویه داخلی و نیمسازهای خارجی دو زاویه دیگر قرار دارد. از این رو، استنباط میگردد که مرکز دایره محاطی داخلی و سه مرکز دایره های محاطی خارجی یک سیستم چهارمرکزی (orthocentric) را تشکیل میدهند. شعاع این دوایر ارتباط نزدیکی با سطح یک مثلث دارد. اگر S سطح مثلث و اضلاع آن b ،a و c باشند، شعاع دایره داخلی ( که "شعاع داخلی" نیز گفته میشود) برابر است با: (S/(2(a+b+c). شعاع دایره خارجی در سمت a برابر است با: (S/(2(-a+b+c)، برای دایره در سمت b برابر است با: (S/(2(a-b+c) و برای دایره در سمت c برابر است با: (S/(2(a+b-c). از این روابط درمیابیم که دوایر خارجی از دایره داخلی بزرگتراند و بزرگترین دایره خارجی، دایره ای است که به بزرگترین ضلع چسبیده است. Triangle with incircle, contact triangle and Gergonne pointمثلث با دایره داخلی (سیاه), مثلث تماس (قرمز)، نقطه جرگونه (سبز) دایره نه نقطه ای مثلث بر سه دایره خارجی و همچنین دایره داخلی مماس میباشد. نقطه فورباخ(Feuerbach) روی دایره داخلی قرار دارد. با علامت گذاری رئوس مثلث با B، A و C و سه نقطه تماس دایره داخلی و مثلث با TB، TA و TC (که TA روبروی A قرار داشته و به همین ترتیب بقیه)، مثلث TATBTC مثلث تماس ABC نامیده میشود. دایره داخلی ABC یک دایره محیطی بر TATBTC میباشد. سه خط BTB ، ATA و CTC در یک نقطه
__________________
|
 |
| کاربران در حال دیدن موضوع: 1 نفر (0 عضو و 1 مهمان) | |
|
|
اکنون ساعت 04:20 PM برپایه ساعت جهانی (GMT - گرینویچ) +3.5 می باشد.





 حالت خطی
حالت خطی

