
|
|
|||||||
| مطالب آزاد در این تالار مطالبی که موضوعات آزاد و متفرقه دارند وجود دارد بدیهیست که کنترل بر روی محتوای این تالار بیشتر خواهد بود |
 |
|
|
ابزارهای موضوع | نحوه نمایش |
|
#1
|
||||
|
||||
 همه چیز در مورد دنباله فیبوناچی
همه چیز در مورد دنباله فیبوناچی
در ریاضیات دنباله فیبوناچی به دنبالهای از اعداد گفته میشود که بصورت زیر تعریف میشود: غیر از دو عدد اول اعداد بعدی از جمع دو عدد قبلی خود بدست میآید. اولین اعداد این سری عبارتاند از: ۰, ۱, ۱, ۲, ۳, ۵, ۸, ۱۳, ۲۱, ۳۴, ۵۵, ۸۹, ۱۴۴, ۲۳۳, ۳۷۷, ۶۱۰, ۹۸۷, ۱۵۹۷, ۲۵۸۴, ۴۱۸۱, ۶۷۶۵, ۱۰۹۴۶ این اعداد به نام لئوناردو فیبوناچی ریاضیدان ایتالیایی نام گذاری شدهاست.فهرست مندرجات [نمایش] دنباله فیبوناچی در دوران حیات فیبوناچی مسابقات ریاضی در اروپا بسیار مرسوم بود در یکی از همین مسابقات که در سال ۱۲۲۵ در شهر پیزا توسط امپراتور فردریک دوم برگزار شده بود مسئله زیر مطرح شد: «فرض کنیم خرگوشهایی وجود دارند که هر جفت (یک نر و یک ماده) از آنها که به سن ۱ ماهگی رسیده باشند به ازاء هر ماه که از زندگیشان سپری شود یک جفت خرگوش متولد میکنند که آنها هم از همین قاعده پیروی میکنند حال اگر فرض کنیم این خرگوشها هرگز نمیمیرند و در آغاز یک جفت از این نوع خرگوش در اختیار داشته باشیم که به تازگی متولد شدهاند حساب کنید پس از n ماه چند جفت از این نوع خرگوش خواهیم داشت.» فرض کنیم xn تعداد جفت خرگوش پس از n ماه باشد، میدانیم که x۲=۱,x۱=۱، تعداد جفت خرگوشها در ماه n+۱ام برابر خواهد بود با حاصلجمع تعداد جفت خرگوشهایی که در این ماه متولد میشوند با تعداد جفت خرگوشهای موجود(xn).اما چون هر جفت خرگوش که از دو ماه قبل موجود بوده هم اکنون حداقل دوماه سن خواهند داشت و به سن زادو ولد رسیدهاند تعداد جفت خرگوشهای متولد شده برابر خواهد بود با xn-۱، پس خواهیم داشت : x۱ = ۱ , x۲ = ۱ , xn + ۱ = xn + xn - ۱ که اگر از قواعد مذکور پیروی کنیم به دنباله زیر خواهیم رسید که به دنباله فیبوناچی مشهور است. ۱, ۱, ۲, ۳, ۵, ۸, ۱۳, ۲۱, ۳۴, ۵۵, ۸۹, ۱۴۴, ۲۳۳, ۳۷۷, ۶۱۰, ۹۸۷, ۱۵۹۷, ۲۵۸۴,… فیبوناچی با حل این مسئله از راه حل فوق دنباله حاصل را به جهان ریاضیات معرفی کرد که خواص شگفتانگیز و کاربردهای فراوان آن تا به امروز نه تنها نظر ریاضیدانان بلکه دانشمندان بسیاری از رشتههای دیگر را به خود جلب کرده. ارتباط عدد طلایی با دنباله فیبوناچی روشهای متفاوتی برای بیان رابطه بین عدد طلایی و دنباله فیبوناچی وجود دارد که ما در اینجا به دو نمونه بسنده می کنیم. نسبت دو عضو متوالی دنباله اولین مطلبی که در زمینه ارتباط با دنباله فیبوناچی قابل ذکر است به این قرار است: دنباله را بار دیگر در نظر می بینیم: ۱۰-------۹--------۸--------۷---------۶-------۵-------۴-------۳-------۲-------۱-------شماره جمله ۵۵------۳۴------۲۱-------۱۳-------۸-------۵-------۳-------۲-------۱-------۱-------مقدار جمله نسبت جمله دوم به اول برابر است با ۱ نسبت جمله سوم به دوم برابر است با ۲ نسبت جمله چهارم به سوم برابر است با ۱٫۵ نسبت جمله پنجم به چهارم برابر است با ۱٫۶۶ نسبت جمله ششم به پنجم برابر است با ۱٫۶ نسبت جمله هفتم به ششم برابر است با ۱٫۶۲۵ نسبت جمله هشتم به هفتم برابر است با ۱٫۶۱۵ نسبت جمله نهم به هشتم برابر است با ۱٫۶۱۹ نسبت جمله دهم به نهم برابر است با ۱٫۶۱۷ به نظر می رسد که این رشته به عدد طلایی نزدیک می شود. اگر نسبت عدد چهلم این رشته را به عدد قبلی حساب کنیم به عدد ۱٫۶۱۸۰۳۳۹۸۸۷۴۹۸۹۵ می رسیم که با تقریب ۱۴ رقم اعشار نسبت طلایی را نشان می دهد. نسبت جملات متوالی به عدد طلایی میل می کند. معادله خط معادله ی خطی به صورت y=mx در نظر می گیریم. m به معنی شیب خط است و یک عدد حقیقی است. می دانیم اگر m گنگ باشد، خط y=mx از هیچ نقطه ای با مختصات صحیح عبور نخواهد کرد. در واقع این خط امکان ندارد از نقطهای (جز مبدأ) عبور کند که هم x و هم y آن عدد صحیح باشند. حال به جای m قرار می دهیمφ. یعنی خط y=φx را در نظر می گیریم. چون φ هم یک عدد گنگ است، این خط از هیچ نقطه ای با x و y صحیح (جز مبدأ) عبور نخواهد کرد. به همین دلیل نقطه هایی را با x و y صحیح در نظر می گیریم که کمترین فاصله را از این خط دارند. ابتدا به نظر می رسد نقطه ی (۱،۱) کمترین فاصله را با این خط دارد. ولی فاصله ی نقطه ی (۲،۱) از این خط کمتر است. نقطه ی (۳،۲) فاصله ی کمتری با این خط دارد. همچنین فاصله ی نقطه ی (۵،۳) از این هم کمتر است. این نقاط به همین ترتیب ادامه خواهند یافت و در زیر چند نقطه ی بعدی را که فاصله شان از این خط کمتر می شود را می بینید: . . . ، (۵،۳۴) ، (۳۴،۲۱) ، (۲۱،۱۳) ، (۱۳،۸) ، (۸،۵) ، (۵،۳) ، (۳،۲) ، (۲،۱) ، (۱،۱) صحت مطالب فوق به راحتی قابل بررسی است. با کمی دقت در مختصات این نقاط درخواهیم یافت که این مختصات از الگوی دنباله فیبوناچی پیروی می کنند . این نقاط را نقاط فیبوناچی می نامند. |
| 3 کاربر زیر از میثاق سپاسگزاری کرده اند برای پست مفیدش: | ||
| جای تبلیغات شما اینجا خالیست با ما تماس بگیرید | |
|
|
|
|
#2
|
||||
|
||||
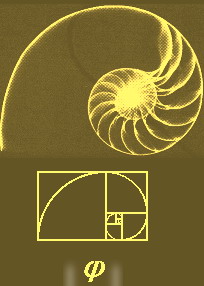
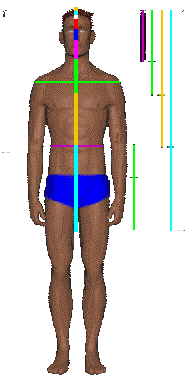
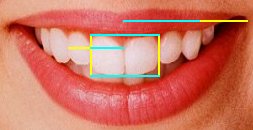
 نکته ی جالب در مورد این دنباله آنکه این دنباله در بعضی دیگر از رویدادهای طبیعی هم قابل مشاهده است.مثلا اگر به گلهایی که داری گلبرگهای زیادند توجه کنید میبینید که تعداد گلبرگهای گل با شروع از وسط گل٬روی هر لایه گلبرگ که به شکل دایره است٬مطابق با همین دنباله زیاد میشود.     در اینجا الگوی رشد برگها رو مشاهده میکنید  و همچنین الگوی رشد گلها  یک عکس جالب هم از آناناس براتون میزارم  اما نکته ی بسیار جالب دیگر در مورد دنباله فیبوناچی اینست که اگر شما هر جمله از این دنباله را به جمله قبلی تقسیم کنید دنباله ی جدیدی حاصل میشود که به عدد ثابت ... ۱.۶۱۸۰۳۳ = ۲/(۵√+۱) همگراست.این عدد ریشه ی مثبت معادله x^۲ - x -1=0 است که به عدد طلایی معروف است.دانشمندان متوجه شده اند که این عدد گنگ در بسیاری از رخدادهای طبیعی ظاهر میشود و اگر ساختاری بر پایه ی این عدد بنا شود از لحاظ انسان ساختاری زیبا تلقی میشود. مثلا در ساخت اهرام مصر(آگاهانه یا ناآگاهانه)از نسبت طلایی استفاده شده    مثالهای طبیعی زیادی نیز در ارتباط با عدد طلایی وجود دارد که نشان میدهد خداوند این جهان را بر پایه ریاضیات بنا کرده است.. اگر قد انسان را بر فاصله کف پا تا ناف تقسیم کنید عدد طلایی حاصل میشود. 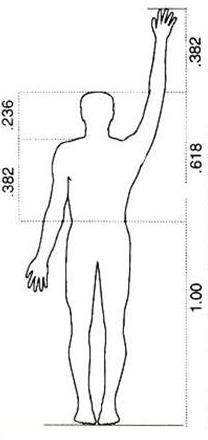 اگر فاصله نوک انگشتان تا آرنج را بر فاصله مچ تا آرنج تقسیم کنید باز هم به عدد طلایی خواهد رسید.  همچنین این نسبت در مارپیچ DNA : مولكول DNA از 2 زنجيره پلي نوكلئوتيدي ساخته شده است. بين بازهاي آلي آدنين و تيمين 2 پيوند هيدروژني و بين بازهاي آلي گوانين و سيتوزين 3 پيوند هيدروژني وجود دارد. 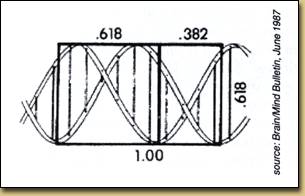 انگشتان : به انگشتان خود نگاه كنيد. 2 دست و هر كدام از آنها 5 انگشت و هر كدام از آنها 3 قسمت مجزا كه توسط 2 بند از هم جدا شده اند. آيا اين تنها يك انطباق است يا خير؟ به هرحال اگر شما استخوان هاي انگشت دست خود را اندازه گيري كنيد (بهترين حالت براي اندازه گيري حالتي است كه انگشتان را خم مي كنيد.) خواهيد ديد كه نسبت طول بزرگترين استخوان انگشت به طول استخوان انگشت با طول متوسط برابر نسبت طلائي است.   و نسبت طول استخوان انگشت با طول متوسط به كوچكترين استخوان انگشت برابر نسبت طلائي است. خدامثل یک نقاش همه جا رو امضاء کرده فقط کافی هست چشمهات رو باز کنی تا دست خطش رو ببینی
__________________
احد،صمد، قاهر، صادق ... عاشقشم لا تقنطوا من رحمة الله هیچ چیز تجربه نمیشه اینو یادت باشه !! ترفند هایی براي ويندوز 7 عیب یابی سخت افزاری سیستم در کسری از دقیقه ویرایش توسط bigbang : 07-12-2011 در ساعت 12:14 PM |
| 2 کاربر زیر از bigbang سپاسگزاری کرده اند برای پست مفیدش: | ||
|
#3
|
||||
|
||||
|
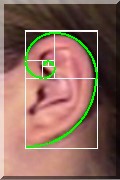
و همچنین در گوشها هم الگوی فیبوناچی دیده میشه
  اگه وقت باشه باز هم میزارم عکس
__________________
احد،صمد، قاهر، صادق ... عاشقشم لا تقنطوا من رحمة الله هیچ چیز تجربه نمیشه اینو یادت باشه !! ترفند هایی براي ويندوز 7 عیب یابی سخت افزاری سیستم در کسری از دقیقه ویرایش توسط bigbang : 07-12-2011 در ساعت 12:12 PM |
| 2 کاربر زیر از bigbang سپاسگزاری کرده اند برای پست مفیدش: | ||
|
#4
|
||||
|
||||
__________________
احد،صمد، قاهر، صادق ... عاشقشم لا تقنطوا من رحمة الله هیچ چیز تجربه نمیشه اینو یادت باشه !! ترفند هایی براي ويندوز 7 عیب یابی سخت افزاری سیستم در کسری از دقیقه |
| 2 کاربر زیر از bigbang سپاسگزاری کرده اند برای پست مفیدش: | ||
|
#5
|
||||
|
||||
|
خوب من اعتراف میکنم دقیقا متوجه پیچیدگی این معادله خاص نشدم
خیلی مسخره است آدم بره یه همچین موردی رو بخونه با یه متن حتی چند صفحه ای بعد بگه کاملا متوجه شدم.... لایک... سپاس !!!!!!!!!!!!!! نه من اونجور آدم نیستم پای فرمول که وسط بیاد ادراک منطق و برهان و شهود و دلیل باید به اون سطح از درک و اثبات و ادله برسه که آدم واقعا قضیه رو درک کنه حقیقتا ادراک یه همچین چیزی از انسان یه ریاضی دان صرف نمیسازه یه عارف و آگاه به علم خلقت میسازه پیرو توضیحات بهتر محمد نسبت به میثاق (ممنونم ازت) چندتا نمونه هم من تو نت پیدا کردم نمونه ها با دقت انتخاب شده روشون شناخت بصری و درکی بهتری داشتم قبلا برام جالب بودن حتی شاید تو ضمیر ناخودآگاه خودم متوجه چیزی خاص تو اینجور چیزها شدم چون خیلی به اینجور مارپیچها (اسپیرالها) علاقه دارم عاشق نقش لچک ترنج هستم حالا میذارم می بینید خیلی عجیبه این فرمول خاص خلقت یه جور معماری و آرایش خاصه قبلشم به خدا بگم فتبارک الله احسن الخالقین    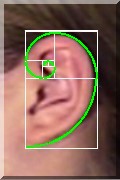  |
|
#6
|
||||
|
||||
|
خیلی عجیبه
خیلی عجیبه خدا وکیلی چیز عجیبیه....      اینو ببینید  عدد بالا رو خوب ببینید همون عدد 1.61950..... خوب حالا متن زیر رو با دقت بخونید عجایب عدد phi و نسبت آن با سری فیبوناچی!
|
 |
| کاربران در حال دیدن موضوع: 1 نفر (0 عضو و 1 مهمان) | |
|
|
اکنون ساعت 05:32 AM برپایه ساعت جهانی (GMT - گرینویچ) +3.5 می باشد.

















 حالت خطی
حالت خطی

