| فنی و مهندسی در این زیر تالار به بحث و گفتگو در مورد رشته های فنی و مهندسی پرداخته میشود |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 تابع
تابع
تابع
در ریاضیات ، تابع رابطهای است که رابطه بین اعضای یک مجموعه را با اعضایی از مجموعهای دیگر (شاید یک عضو از مجموعه) را بیان میکند. نظریه درباره تابع یک پایه اساسی برای خیلی از شاخههای ریاضی به حساب میآید. مفاهیم تابع ، نگاشت و تبدیل معمولاً مفاهیم مشابهای هستند. عملکرد ها معمولاً دو به دو بین اعضای تابع وارد عمل میشوند.
تعریف تابع
در ریاضیات تابع عملکردی است که برای هر ورودی داده شده یک خروجی منحصر بفرد تولید میکند معکوس این مطلب را در تعریف تابع بکار نمیبرند. یعنی در واقع یک تابع میتواند برای چند ورودی متمایز خروجیهای یکسان را نیز تولید کند. برای مثال با فرض y=x2 با ورودیهای 5- و 5 خروجی یکسان 25 را خواهیم داشت. در بیان ریاضی تابع رابطهای است که در آن عنصر اول به عنوان ورودی و عنصر دوم به عنوان خروجی تابع جفت شده است.
به عنوان مثال تابع f(x)=x2 بیان میکند که ارزش تابع برابر است با مربع هر عددی مانند x
در واقع در ریاضیات رابطه را مجموعه جفتهای مراتب معرفی میکنند. با این شرط که هرگاه دو زوج با مولفههای اول یکسان در این رابطه موجود باشند آنگاه مولفههای دوم آنها نیز یکسان باشد. همچنین در این تعریف خروجی تابع را به عنوان مقدار تابع در آن نقطه مینامند. مفهوم تابع اساسی اکثر شاخههای ریاضی و علوم محاسباتی میباشد. همچنین در حالت کلی لزومی ندارد که ما بتوانیم فرم صریح یک تابع را به صورت جبری آلوگرافیکی و یا هر صورت دیگر نشان دهیم.
فقط کافیست این مطلب را بدانیم که برای هر ورودی تنها یک خروجی ایجاد میشود در چنین حالتی تابع را میتوان به عنوان یک جعبه سیاه در نظر گرفت که برای هر ورودی یک خروجی تولید میکند. همچنین لزومی ندارد که ورودی یک تابع ، عدد و یا مجموعه باشد. یعنی ورودی تابع را میتوان هر چیزی دلخواه در نظر گرفت البته با توجه به تعریف تابع و این مطلبی است که ریاضیدانان در همه جا از آن بهره میبرند.
تاریخچه تابع
نظریه مدرن توابع ریاضی بوسیله ریاضیدان بزرگ لایب نیتر مطرح شد همچنین نمایش تابع بوسیله نمادهای (y=f(x توسط لئونارد اویلر در قرن 18 اختراع گردید، ولی نظریه ابتدایی توابع به عنوان عملکرهایی که برای هر ورودی یک خروجی تولید کند توسط جوزف فوریه بیان شد. برای مثال در آن زمان فوریه ثابت کرد که هر تابع ریاضی سری فوریه دارد.
چیزی که ریاضیدانان ما قبل اوبه چنین موردی دست نیافته بودند، البته موضوع مهمی که قابل ذکر است آنست که نظریه توابع تا قبل از بوجود آمدن نظریه مجموعهها در قرن 19 پایه و اساس محکمی نداشت. بیان یک تابع اغلب برای مبتدیها با کمی ابهام همراه است، مثلا برای توابع کلمه x را به عنوان ورودی و y را به عنوان خروجی در نظر میگیرند ولی در بعضی جاها y,x را عوض میکنند.
ورودی تابع
ورودی یک تابع را اغلب بوسیله x نمایش میدهند. ولی زمانی که ورودی تابع اعداد صحیح باشد. آنرا با x اگر زمان باشد آنرا با t ، و اگر عدد مختلط باشد آنرا با z نمایش میدهند. البته اینها مباحثی هستند که ریاضیدانان برای فهم اینکه تابع بر چه نوع اشیایی اثر میکند بکار میرود. واژه قدیمی آرگومان قبلا به جای ورودی بکار میرفت. همچنین خروجی یک تابع را اغلب با y نمایش میدهند در بیشتر موارد به جای f(x) , y گفته میشود. به جای خروجی تابع نیز کلمه مقدار تابع بکار میرود. خروجی تابع اغلب با y نمایش داده میشود. ولی به عنوان مثال زمانی که ورودی تابع اعداد مختلط باشد، خروجی آنرا با "W" نمایش میدهیم. (W = f(z
تعریف روی مجموعهها
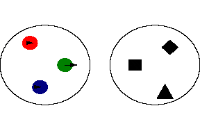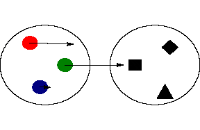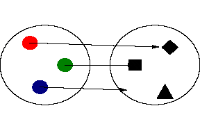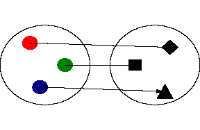
یک تابع رابطهای منحصر به فرد است که یک عضو از مجموعهای را با اعضای مجموعهای دیگر مرتبط میکند. تمام روابط موجود بین دو مجموعه نمیتواند یک تابع باشد برای روشن شدن موضوع ، مثالهایی در زیر ذکر میکنیم:
این رابطه یک تابع نیست چون در آن عنصر 3، با دو عنصر ارتباط دارد. که این با تعریف تابع متناقص است چون برای یک عنصر از مجموعه، دو عنصر در مجموعه موجود است
- این رابطه یک تابع یک به یک است. چون به ازای هر x یک y وجود دارد.
تعریف ساخت یافته تابع
بطور ساخت یافته یک تابع از مجموعه x به مجموعه y بصورت f:x→y نوشته میشود و به صورت سه تایی مرتب ( (x,y,G(f) نمایش داده میشود. بطوری که (G(f زیر مجموعهای از حاصلضرب کارتزین xy میباشد. با این شرط که به ازای هر x در X یک Y متعلق به Y نسبت داد شود. با این شرط زوج مرتب (x,y) را در داخل (G(f میپذیریم. در این حالت نیز X را به عنوان دامنه f و y را به عنوان برد fو (G(f را به عنوان نمودار و یا گراف تابع F در نظر میگیرند.
خواص توابع
توابع میتوانند:
- زوج یا فرد باشند.
- پیوسته یا ناپیوسته باشند.
- حقیقی یا مختلط باشند.
- اسکالر یا برداری باشند.
توابع چند متغیره
یک تابع ممکن است بیشتر از یک متغیر داشته باشد برای مثال یک تابع از f است که دارای سه پارامتر x,y,z است که یک ارزش را برای تابع تولید میکنند. از توابع چند متغیره میتوان به قانون جاذبه نیوتن اشاره کرد که در آن دو جرم با متغیر و و نیز یک متغیر برای فاصله هر جرم به نام در آن وجود دارد.
با مقدار دهی به سه پارامتر فوق مقدار تابع F محاسبه خواهد شد.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |
|
جای تبلیغات شما اینجا خالیست با ما تماس بگیرید
|
|

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 مفهوم تابع
مفهوم تابع
مفهوم تابع
دید کلی
مفهوم تایع یکی از مهم ترین مفاهیم علم ریاضی بوده و به همان اندازه در ریاضی اهمیت دارد که مفهوم مجموعه دارد. اغلب، می گویند تابع، کمیت متغیری است که از کمیت متغیر دیگر تبعیت می کند. برای توزیع "معمولی"، مانند:
Y=sinx ,y=x2 , y=a+bx
والی آخر، این تعریف کاملا مناسب می باشد. ممکن است اگر توابع دیگری، مانند: y=sin2x+cos2x
را در نظر بگیریم، می بینیمی که مقادیر آن تابعه دیگر تغییر نمی کند و بنابراین دیگر کمیت متغیری که از کمیت x تبعیت کند، وجود نداد.
! تعریف تایع:
تناظری که به هر عنصر x از یک مجموعه x فقط و فقط یک عنصر y از یک مجموعه y رانسبت را دهد، تایع گویند. توابع را با حروف f یا حروف کوچک خطی لاتین نشان می دهیم.
مفهوم تابع از دیدگاه دیگری
از طرفی، تحت عنوان کمیت "چیزهایی" را در نظر می گیرند که آنها همه با هم قابل مقایسه باشند. یعنی "چیزهایی که" بین آن ها روابط "بیشتر" و "کم تر" و.جود دارد.
در صورتی که در ریاضیات، توابعی نیز مطالعه می شود که برای آنها این روابط تعیین نشده است، مثلا به عنوان مثال از اعداد کمپلکس (مختلط) یا به طور کلی از عناصر یک مجموعه دلخواه می توان اسم برد. توجه دقیق نشان می دهد که در مفهوم تابع وابستگی تغییرات به تغییرات متغیر مستقل آنم اندازه مهم نیست که تناظر بین مقادیر متغیر مستقل و مقادیر تابع مهم می باشد. به خصوص اگر به خاطر بیاوریم که تمامی اطلاعات راجع به تابع، می تواند از بیان گرافیکی آن استخراج گردد، و در نتیجه نباید فرض بین بیان گرافیکی تابع و خود تابع قائل شده و از طرفی
رافیک تابع مجموعه نقاطی است که هر یک از آن ها با دو مختصات y,x یعنی با (x,y) مشخص میگرند. بدین ترتیب به نظر می رسد که در تعریف تابع، مناسب است از آن خصوصیات مجموعه زوج های مرتب استفاده گردد که ویژه گرافیک تابع باشند.
قلمرو و برد تابع:
مجموعه x را قلمرو تابع و مجموعه y را برد تابع f می نامند. تابعf را از مجموعه x به مجموعه y را معمولا به صورت f:x→y y=f(x)
نشان می دهند.
مثال هایی از تابع:
1) تبدیل درجه فارنهایت به سانتیگراد را در نظر می گیریم برای هر عدد حقیقی x، درجه فارنهایت معادل است با:
درجه سانتیگراد.
فرض می کنیم y,x هر دو عدد مجموعه اعداد حقیقی باشند، در نتیجه این عمل، به هر عنصر x از مجموعه Xعنصر یگانه f(x) از مجموعه y را نظیر می کند. اگر داشته باشیم:
پس نتیجه می گیریم برای هر مقدار x یک مقدار x از منحصر بفردی y موجود است.
f(32)=0 f(68)= 0 f(212)=0
مفهوم تابع برای سه تایی مرتب:
اگر در نظر بگیریم که خود متناظر به توسعه 3- تایی مرتب مجموعه هایی است که9 جزو اول آن زیر مجموعه از حاصل ضرب مستقیم جز دوم و سوم آن می باشد و بین عناصر این حاصل ضرب زوج هایی که اجزا اول آنها یکسان و اجزا دوم آن ها متفاوت باشند. وجود ندارد، یعنی اگر (x,z),(x,y) عناصر حاصلضرب مستقیم باشند، آنگاه y=z خواهد بود. بنابراین طبق تعریف:
3- تایی (f,x,y) را تابع گویند، هر گاه:
(1) باشد.
(2) F زوج هایی نداشته باشد که اجزا اول ان ها یکسان و اجزا دوم آن ها متقارن باشند.
گراف تابع:
در تابع f:X→Y مجموعه تمامیزوج هائی که اجزای اول آن ها را عناصر مجموعه X و اجزای دوم آن ها را تصویر عناصر مجموعه X تشکیل می دهند، گراف تابع خواهد بود.
مفاهیم مربوط به تابع:
برای توابع مفاهیمی مانند "گراف تابع"، "ناحیه مبدا تابع"، "ناحیه تعریف تابع"، "ناحیه مقادیر تابع" ظاهر می شود چون برای تابع، ناحیه تعریف با ناحیه مبدا منطبق می شود، بدین جهت برای تابع فقط ناحیه تعریف را به تنهایی به کار می برند. تابه f را با ناحیه تعریف x ناحیه مقصد y تابعی را "نوع x→y" می نامند.
تعبیر هندسی تابع:
f تابع است اگر خطی موازی محور y ها رسم کنیم منحنی تابع را فقط و فقط در یک نقطه قطع کند. یعنی به ازای یک y فقط و فقط یک x داشته باشیم.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری
ویرایش توسط رزیتا : 10-28-2009 در ساعت 08:20 PM
|

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 اعمال جبری روی توابع
اعمال جبری روی توابع
اعمال جبری روی توابع
دید کلی
برای توابع نیز مانند مجموعهها ، یا خود تناظرها میتوان عملیات جبری را تعریف نمود که باید تابع مورد نظر ، تابع حقیقی باشد. منظور از یک تابع با مقدار حقیقی روی مجموعه X، یا به طور خلاصه ، یک تابع حقیقی روی مجموعه X تابعی است مانند f: X→R از مجموعه X به مجموعه اعداد حقیقی، تابع مختلط نیز به طریق مشابهی تعریف میشود.
مجموعه دلخواه X را در نظر میگیریم؛ فرض میکنیم مجموعه کلیه توابع حقیقی روی مجموعه X باشد. برای این توابع حقیقی ، اعمال جمع و ضرب را نظیر اعمال جمع و ضرب در اعداد حقیقی میتوان تعریف نمود.
تعریف جمع دو تابع
حاصل جمع دو تایی حقیقی f: X→R و g: X→R برابر است با تابع حقیقی f+g: X→R
به طوری که برای هر ، مقدار x تحت تابع f+g مساوی است با حاصل جمع دو عدد حقیقی و به عبارت دیگر ، برای هر داریم:
=+
تعریف ضرب دو تابع
حاصلضرب دو تابع حقیقی f: X→R و g: X→R عبارت است از تابع حقیقی
fg: X→R
به طوری که برای هر مقدار x تحت تابع fg برابر است با حاصلضرب دو عدد حقیقی و . به عبارت دیگر، برای هر داریم:
=x
- هرگاه تعداد عناصر مجموعه X باپایان باشد، با جمع و ضرب عناصر متناظر در جدول تناظر توابع g , f ، به آسانی میتوان جدول تناظر توابع f+g و fg را تشکیل داد.
ویژگیهای مهم حاصلجمع تابعی و حاصلضرب تابعی
حاصلجمع و حاصلضرب توابع حقیقی را به ترتیب حاصلجمع تابعی و حاصلضرب تابعی مینامیم. چون حاصلجمع و حاصلضرب توابع حقیقی براساس حاصلجمع و حاصلضرب اعداد حقیقی تعریف شدند، به سهولت خواص و ویژگیهای زیر را از اعداد حقیقی به ارث میبرند.
حاصلجمع تابعی و حاصلضرب تابعی توابع حقیقی دارای ویژگیهای زیر میباشند: - خاصیت جابجایی: برای دو تابع حقیقی g ,f روی مجموعه X داریم:
f+g=g+f
fg=gf - خاصیت شرکت پذیری: برای سه تابع f، g و h روی مجموعه X داریم:
- خاصیت پخش پذیری: برای سه تابع f، g و h روی مجموعه X داریم:
=+
حاصلضرب تابع حقیقی در یک عدد حقیقی (حاصل ضرب اسکالر)
حاصلضرب عدد حقیقی C و تابع حقیقی f: X→R عبارت است از تابع حقیقی
Cf: X→R
به طوری که برای هر مقدار تابع برابر است با حاصلضرب دو عدد حقیقی C و
خواص حاصلضرب اسکالر
ویژگیهای مهم حاصلضرب عددی توابع حقیقی عبارتند از:
=af+ag
=af+bf
=
=
If=f
که در روابط بالا b , a اعداد حقیقی دلخواه و g , f توابع حقیقی دلخواهی روی مجموعه X میباشند.
تفاضل دو تابع حقیقی
تفاضل دو تابع حقیقی f: X→R و g: X→R را میتوان بر حسب حاصلضرب عددی و حاصلجمع تابعی به وسیله رابطه
f-g=f+(-1)g
یا مستقیما، برای هر به وسیله:
=-
تعریف نمود. تفاضل f-g تابعی حقیقی روی مجموعه X میباشد.
خارج قسمت دو تابع حقیقی
خارج قسمت تابع حقیقی f: X→R بر تابع حقیقی g: X→R را میتوان برای هر به صورت
تعریف نمود. باید توجه داشت که تابع خارج قسمت (f/g) وقتی معین یا تعریف شده است که برای هر داشته باشیم g(x)≠0. بنابراین خارج قسمت f/g تابعی حقیقی روی مجموعه X میباشد.
توانهای صحیح تابع حقیقی
توانهای صحیح تابع حقیقی f: X→R یا به عبارت دیگر fn به این صورت تعریف میشود. هرگاه n>0 ، آنگاه fn ، تابع حقیقی بر روی مجموعه X است. که برای هر با ضابطه
تعریف میشود. اگر n≤0، آنگاه برای هر باید داشته باشیم ، در این صورت ، fn برای هر به صورت
تعریف میشود.
بنابراین، برابر تابع ثابت 1 روی مجموعه X خواهد بود.
خواص توانهای صحیح تابع
خواص توانهای صحیح حقیقی f: X→R، مستقیما از ویژگیهای متناظر اعداد حقیقی نتیجه میشود:
تعریف دامنه
برای توابع جبری که ساختیم باید دامنه تعریف کنیم. دامنه توابع در زیر آمده است:
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 تابع یک به یک و پوشا
تابع یک به یک و پوشا
تابع یک به یک و پوشا
دید کلی:
تابع f:x→y را در نظر می گیریم. منظور از تابع f، تصویر قلمرو آن است. یعنی مجموعه f(x)={f(x)│
معمولا تصویر تابع f:x→y را با نماد Im(f) نشان می دهند: بنابراین داریم: Im(f)=f(x)
به عنوان مثال، اگر تابع f، تصویر جانور x به وسیله نور آفتاب بر روی دیوار y باشد، آنگاه تصویر تابع f یعنی Im(f) برابر سایه جانور بر روی دیوار خواهد بود.
در حالت کلی، در مورد تابع دلخواه f(x), f:x→y معمولا با y براتبر نیست. مثلا درمثال تصویر جانور x به وسیله نور آفتاب بر روی دیوار y، سایه جانور یعنی f(x) معمولا نباید تمام دیوار را بپوشاند. البته امکان دارد که برای تابعی داشته باشیم.
در این حالت f را تابعی از مجموعه x به روی مجموعه y یا به طور خلاصه f را پوشا می نامیم.
تعریف تابع پوشا
تابع f:x→y را پوشا می نامیم اگر تنها f(x)=y
تعریف کلی برای تابع پوشا یا تابع در روی مجموعه ها:
گیریم f تابعی است که ناحیه تعریف آن x و ناحیه مقصد آن y باشد، یعنی تصویر x به توی y باشد:
در اینصورت مقادیر این تابع که آن ما با f(x) نشان می دهیم، یک زیر مجموعه ای است از مجموعه y ، یعنی f(x) cy یعنی اگر ناحیه مقصد y و ناحیه مقادیر تابع f(x) یکسان باشند، در اینصورت f تابعی از x در روی y است یا f "x را در روی y تصویر می کند". یا به طور ساده گویند f یک تابع پوششی است.
در این حالت از تابع هریک از عناصر ناحیه مقصد، افلا تصویر یکی از عناصر ناحیه تعریف تابع (x) می باشند.
مثالی از تابع پوشا:
1) تابع جز صحیح Ө:R→Z از مجموعه اعداد حقیقی به مجموعه اعداد صحیح که هر عدد حقیقی x را به جز صحیح x نظیر می کند.
Ө(x)=x
پوشاست. ولی تابع قدر مطلق α:R→R از مجموعه اعدادحقیقی به خودش که هر عدد حقیقی x را به قدر مطلق آن نظیر می کند.
Α(x)=│x│
پوشا نیست. چون اگر منحنی تابع قدر مطلق را رسم کنیم این منحنی فقط اعداد حقیقی مثبت را شامل میشود که با تعریف تابع قدر مطلق که تمام اعداد حقیقی را شامل میشود تناقص دارد. پس تابع قدر مطلق پوشا نیست.
تابع یک به یک:
تابع دلخواه f:x→y را در نظر می گیریم. فرض می کنیم b,a دو عنصر دلخو.اه متعلق به قلمرو f باشند. بر حسب تعریف تابع، تصاویر f(b),f(a) می توانند هر عنصری از مجموعه y یا برد f باشند. بنابراین ممکن است داشته باشیم.
F(a)=f(b)
مثلا تابع قدر مطلق α:R→R را در نظر می گیریم. واضح است که برای هر عدد حقیقی a داریم
Α(a)=a(-a)
البته ممکن است که برای تابع خاص f:x→y به ازای هیچ دو عنصر b,a از قلمرو f، تساوی امکان پذیر نباشد. توابعی را که دارای ان خاصیت مهم باشند، یک به یک می نامیم.
تعریف تابع یک به یک:
تابع f:x→y را یک به یک می نامیم، اگر و تنه اگر، تصاویر عناصر متمایز قلمرو f متمایز باشند. به عبارت دیگر، تابع f:x→y یک به یک است اگر و تنها اگر برای هر دو عنصر دلخواه x2,x1 از قلمرو f که f(x1)=f(x2) نتیجه شود a=b مثلا، تابع شمول i:x→y که و برای هر با ضابطه تعریف می شود، تابعی یک به یکی است. در حالی که هیچ یگ از تواغبع جز صحیح Ө:R→Z و قدرمطلق α:R→R، یک به یک نیستند.
تشخیص یک به یک بودن:
اگر f یک به یک باشد، هر خط موازی محور x ها را حداکثر در یک نقطه قطعه می کند. در غیر این صورت f یک به یک نخواهد بود.
تابع دوسویی:
تابع f:x→y را دو سویی می نامیم، اگرو تنها اگر یک به یک و پوشا باشد.
به عنئوانمثال: تابع f:R→R که درجه فارنهایت را به درجه سانتیگراد تبدیل می کند تابع دو سویی است برای هر مجموعه دلخواه x، تابع همانی i:x→x که برای هر با ضابطه i(x)=x تعریف می شود، تابعی دو سویی است. یعنی هم یک به یک و هم پوشا می باشد.
رابطه یک به یک بودن با صعودی یا نزولی بودن:
اگر تابع f صعودی یا نزولی باشد، آنگاه یک به یک خواهد بود. ولی هر تابع یک به یک، صعودی یا نزولی نیست.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 تابع همانی
تابع همانی
تابع همانی
تابع همانی:
می دانیم یک رابطه همانی روی مجموعه A رابطه ای است که برای هر عضو از مجموعه A چون a تنها شامل زوج مرتب باشد و هیچ زوج مرتبی با مولفه های متمایز نداشته باشد. این رابطه را به این صورت تعریف می کنیم:
این رابطه روی مجموعه A یک تابع است که به آن تابع همانی می گوییم. این تابع هر عضو از دامنه خود را به خودش متناظر می کند. اگر f تابعی همانی از مجموعه A در A باشد، آن را به این صورت تعریف می کنیم:
پس ضابطه تابع همانی به این صورت است:
اثبات تابع بودن رابطه همانی:
اگر f رابطه همانی روی مجموعه A به صورت مقابل باشد: برای اثبات تابع بودن این رابطه کافی است نشان دهیم:
واضح است که:
پس این رابطه تابع است. - از آنجا که معمولا در حساب دیفرانسیل و انتگرال با اعداد حقیقی و توابع حقیقی کار می کنیم معمولا تعریف زیر را برای تابع همانی استفاده می کنیم:
تابع را با ضابطه تابع همانی می گوییم.
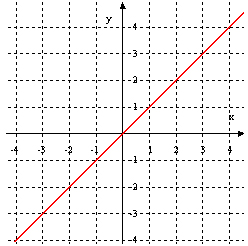
نمودار این تابع بسته به دامنه تابع می تواند نیمساز ربع اول و سوم یا قسمتی از آن باشد.
اگر دامنه این تابع مجموعه اعداد حقیقی باشد نمودار این تابع نیمساز ربع اول و سوم خواهد بود که در زیر نمودار آن را مشاهده می کنید:
- بررسی ویژگی های تابع همانی:
- تابع همانی تابعی است که معکوس آن با خودش برابر است.
برهان: کافی است نشان دهیم اگر آنگاه برای اثبات از روش یافتن وارون(معکوس) تابع استفاده می کنیم:
مشاهدی می شود معکوس این تابع با خودش برابر است.
این مطلب از نظر هندسی هم واضح است چرا که می دانیم برای یافتن نمودار معکوس تابع می توان نمودار آن تابع را نسبت به نیمساز ربع اول و سوم قرینه نمود، حال آنکه قرینه تابع همانی نسبت به نیمساز ربع اول و سوم همان نیمساز ربع اول و سوم(خود تابع) است که نشان می دهد معکوس این تابع با خودش برابر است.
- تابع همانی تابعی فرد است.
برهان: باید نشان دهیم
داریم:
همچنین نمودار این تابع نسبت به مبدا مختصات متقارن است که دلیل بر فرد بودن این تابع است.
- تابع همانی تابعی یک به یک و پوشا است پس می توان گفت این تابع یک تابع دو سویی(تناظر یک به یک) است.
برهان: ابتدا نشان می دهیم این تابع، تابع یک به یک است:
به این منظور باید نشان دهیم:
اگر باشد طبق تعریف داریم: و از این عبارت نتیجه می شود که: . پس رابطه همانی یک تابع یک به یک است.
حال نشان می دهیم این تابع پوشا است یعنی برای هر عضو در برد تابع عضوی متناظر در دامنه وجود دارد که آن عضو در دامنه به آن عضو در برد نظیر می شود. با توجه به اینکه برد و دامنه این تابع مجموعه اعداد حقیقی است باید نشان دهیم:
و چون دامنه و برد این تابع برابر است می توان گفت x یافت شده (برای هر y) در دامنه وجود دارد. پس تابع پوشا است.
حال چون تابع همانی هم یک به یک و هم پوشا است می توان گفت این تابع دو سویی است.
- یادآودی: تابع f را دوسویی با تناظر یک به یک می گوییم هرگاه یک به یک و پوشا باشد.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 تابع ثابت
تابع ثابت
تابع ثابت:
تابع را تابع ثابت می گوییم هر گاه برد آن یک مجموعه تک عضوی باشد. به عبارت دیگر تابع ثابت هر عضو از دامنه خود را تنها به یک مقدار ثابت متناظر می کند.
پس ضابطه تابع ثابت f از مجموعه A در مجموعه B را می توان به این صورت نوشت که در آن c مقداری ثابت و همان برد تابع f است.
به عنوان مثال تابع یک تابع ثابت است که هر عضو از دامنه خود(مجموعه اعداد حقیقی) را به عدد ثابت 2 متناظر می کند و عدد دو همان برد تابع است.
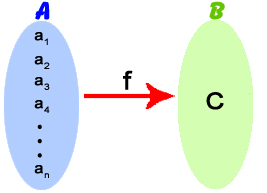
نمودار پیکانی زیر نحوه عملکرد تابع ثابت را نشان می دهد:
مشاهده می شود این تابع هر عضو از دامنه(A) خود را به یک مقدار ثابت c متناظر می کند.
به عبارت دقیق تر تابع فوق یک تابع ثابت از مجموعه A به مجموعه تک عضوی {c} است که می توان این مطلب را اینگونه نوشت:
تابع با ضابطه
- به دلیل اینکه در حساب دیفرانسیل و انتگرال معمولا با توابع حقیقی و اعداد حقیقی کار می کنیم تابع ثابت معمولا به این صورت تعریف می شود:
تابع با ضابطه را تابعی ثابت می گوییم. این تابع هر عدد حقیقی را به یک مقدار ثابت چون c متناظر می کند.
نمودار تابع یک تابع ثابت همواره یک خط موازی محور X ها است. به عنوان مثال نمودار تابع ثابت به این صورت است:
- بررسی ویژگی های توابع ثابت:
- توابع ثابت توابعی غیر یک به یک می باشند.
برهان: تابع ثابت هر عضو از دامنه خود را به C متناظر می کند پس: که این نشان می دهد تابع ثابت یک به یک نمی باشد چرا که دو زوج مرتب با مولفه اول متمایز و با مولفه دوم یکسان در آن یافت می شود.
- توابع ثابت معکوس پذیر نمی باشند.
برهان: می دانیم شرط لازم و کافی برای اینکه تابعی معکوش پذیر باشد این است که یک به یک باشد. حال آنکه تابع ثابت یک به یک نمی باشد. پس معکوس پذیر هم نمی باشد. به عبارت دیگر عمل معکوس یک تابع ثابت دیگر یک تابع نمی باشد.
- تابع ثابت تابعی پوشا است.
برهان: تابع ثابت را در نظر بگیرید. برای اثبات پوشا بودن باید نشان داد:
حال در تابع ثابت داریم:
که این نشان می دهد برای هر عضو از برد یعنی C یک عضو از دامنه چون x وجود دارد که x به C متناظر شود یا به عبارتی که این دلیل بر پوشا بودن f است.
- تابع ثابت زوج می باشند به استثنای تابع که هم زوج و هم فرد است.
برهان: تابع ثابت را در نظر بگیرید. دامنه این تابع مجموعه اعداد حقیقی است. لذا شرط اولیه زوج یا فرد بودن تابع یعنی متقارن بودن دامنه را دارا است.
پس تابع مذکور زوج است.
حال تابع را در نظر بگیرید. داریم:
همچنین می توان نوشت:
پس تابع مذکور هم در شرط زوج بودن و هم در شرط فرد بودن تابع صدق می کند پس هم زوج و هم فرد است.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 تابع علامت
تابع علامت
تابع علامت:
تابع با ضابطه زیر را تابع علامت می گوییم:
لازم به ذکر است که این تابع را با نماد نشان می دهند که نماد آن از واژه انگلیسی sign اقتباس شده است که ریشه اصلی آن، از واژه یونانی signum به معنای علامت است.
همچنین ضابطه این تابع را برای X های مخالف صفر می توان اینگونه تعریف کرد:
در این تابع دامنه مجموعه اعداد حقیقی است و برد این تابع برابر است با: .
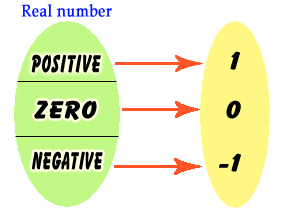
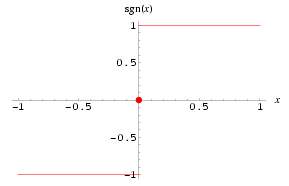
این تابع از معروف ترین توابع چند ضابطه ای است که نحوه عملکرد آن به این صورت است: - اگر متغییر x داده شده به تابع مثبت باشد آن را به عدد یک و اگر متغییر x داده شده به تابع منفی باشد آن را به منفی یک متناظر می کند و اگر متغییر داده شده x=0 باشد آن را به عدد صفر متناظر می کند. به عبارت دیگر این تابع هر عدد حقیقی مثبت را به یک، هر عدد حقیقی منفی را به منفی یک متناظر می کند و عدد صفر را هم به صفر متناظر می کند.
- نمودار پیکانی زیر نحوه عملکرد تابع علامت(sgn) را نشان می دهد:
- با توجه به ضابطه این تابع نمودار آن به این صورت خواهد بود:
- بررسی ویژگی های تابع علامت
- تابع علامت تابعی فرد است.
برهان: تابع را در نظر بگیرید:
که این نشان می دهد این تابع فرد است. همچنین نمودار این تابع نسبت به مبدا مختصات متقارن است که دلیل بر فرد بودن تابع است.
- تابع علامت تابعی غیر یک به یک است.
برهان: در توابع چند ضابطه ای شرط اولیه برای یک به یک بودن تابع این است که هر ضابطه یک به یک باشد اما مشاهدی می شود در مورد تابع علامت این شرط برقرار نمی باشد. پس این تابع یک به یک نمی باشد.
- تابع علامت تابع پوشا است.
برهان: می دانیم در بررسی پوشا بودن توابع چند ضابطه ای به این صورت عمل می کنیم که برد هر ضابطه را محاسبه کرده اجتماع آنها را بدست می آوریم. اگر حاصل با مجموعه انجام تابع برابر باشد تابع پوشا است. حال در تابع علامت اجتماع بردهای هر ضابطه برابر با مجموعه است(چرا؟).
و چون با مجموعه انجام تابع یعنی برابر است پس این تابع پوشا است.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 تابع دیریکله(Dirichlet Function)
تابع دیریکله(Dirichlet Function)
تابع دیریکله(Dirichlet Function)
اگر c و d دو عدد حقیقی متمایز باشند آنگاه تابع دیریکله را چنین تعریف می کنند:
این تابع چندضابطهای را با نماد (D(x نشان می دهند و معمول ترین و صورت آن حالتی است که C=1 و d=0 باشد که در این صورت تابع دیریکله به این صورت تعریف می شود:
تعریف فوق از تابع دیریکله را همچنین میتوان با استفاده از آنالیز ریاضی به این صورت نشان داد:
به عنوان مثال:
اگر x=2 باشد آنگاه:
و اگر به جای x عدد پی که گنگ است را قرار دهیم:
اما چون لذا تابع دیریکله را میتوان به عنوان تابع مشخصهاعداد گویا در مجموعه اعداد حقیقی در نظر گرفت.
از جمله ویژگی های مهم تابع دیریکله این است که در هیچ نقطه و بازه ای دارای حد نمیباشد، پیوسته و انتگرال پذیر هم نمیباشد.. به این ترتیب نموداری از آن نمیتوان رسم کرد.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 توابع زوج و فرد:
توابع زوج و فرد:
توابع زوج و فرد:
فرض کنید f تابعی با دامنه با شد و برای هر آنگاه باشد(در اصطلاح دامنه تابع f متقارن باشد). در این صورت: - تابع f را زوج می گوییم هرگاه:
- تابع f را فرد می گوییم هرگاه:
اگر هیچ یک از شرایط فوق برقرار نباشد تابع را نه زوج و نه فرد می گوییم. - توجه کنید که شرط اولیه اینکه تابعی بتواند زوج یا فرد باشد این است که دامنه اش متقارن باشد یعنی:
و اگر شرط فوق برقرار نباشد در مورد زوج یا فرد بودن تابع بحث نمی شود.(چرا؟)
به عنوان مثال تابع تابعی است نه زوج و نه فرد چرا که دامنه اش برابر است با که متقارن
نمی باشد چون 1- عضو دامنه بوده ولی 1 عضو دامنه نمی باشد و شرط اولیه برای زوج یا فرد بودن تابع برقرار نمی باشد.
به عنوان مثال تابع تابعی زوج است چرا که اولا وامنه اش مجموعه اعداد حقیقی بوده پس متقارن است و همچنین داریم:
و همچنین تابع تابعی فرد است چرا که دامنه اش مجموعه اعداد حقیقی بوده و متقارن است و همچنین:
تابع هم تابعی نه زوج و نه فرد است زیرا البته شرط اولیه یعنی متقارن بودن دامنه برقرار است) که در هیچ یک از شراط تابع زوج یا فرد صدق نمی کند. البته شرط اولیه یعنی متقارن بودن دامنه برقرار است) که در هیچ یک از شراط تابع زوج یا فرد صدق نمی کند.
- بررسی زوج و فرد بودن تابع از روی نمودار تابع:
- از نظر هندسی نمودار تابع زوج نسبت به محور y ها متقارن است.
برهان: می دانیم در تقارن یک نقطه نسبت به محور y ها مولفه y ثابت و مولفه x قرینه می شود پس زمانی نسبت به محور y ها متقارن است که با تبدیل x به x- تابع تغییری نکند. پس در چنین تابعی داریم: که این همان تعریف تابع زوج است.
به عنوان مثال نمودار تابعی که در بالا زوج بودنش را نشان دادیم به این صورت است:
مشاهده می کنید این تابع نسبت به محور Y ها متقارن است. - از نظر هندسی نمودار تابع فرد نسبت به مبدا مختصات متقارن است.
برهان: می دانیم در تقارن یک نقطه نسبت به مبدا همه مولفه ها قرینه می شوند. پس تابع هنگامی نسبت به مبدا متقارن است که با تبدیل x به x- تابع از (f(x به (f(x- تغییر کند. پس در چنین تابعی داریم: که این همان تعریف تابع فرد است.
به عنوان مثال نمودار تابعی که در بالا فرد بودنش را بررسی کردیم به این صورت است:
مشاهده می شود این تابع نسبت به مبدا متقارن است.
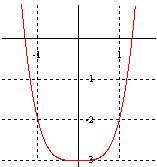
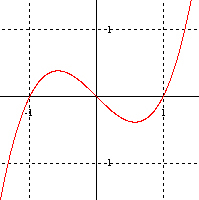
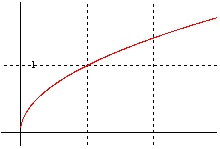
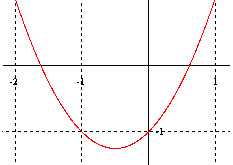
تابعی که هیچ یک از این ویژگی ها را نداشته باشد نه زوج و نه فرد است. به عنوان مثال نمودار های زیر نمونه ای از نمودار های توابع نه زوج و نه فرد است:
از معروف ترین توابع نه زوج و نه فرد می توان به تابع هموگرافیک و تابع لگاریتم اشاره کرد.
- حال ممکن است این سوال پیش بیاید که آیا تابعی وجود دارد که هم زوج و هم فرد باشد؟
بررسی می کنیم:
اگر چنین تابعی موجود باشد خاصیت زوج بودن و فرد بودن را با هم دارد. فرض کنید تابع با دامنه دارای چنین خاصیتی باشد و
داریم:
حال با جمع کردن طرفین:
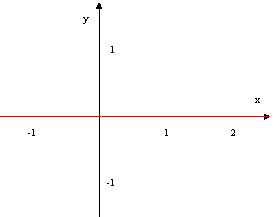
پس تابع (محور Xها) تنها تابعی است که هم زوج و هم فرد است و نمودار آن به این صورت است:
مشاهده می کنید که نمودار این تابع هم نسبت به مبدا مختصات و هم نسبت به محور Y ها متقارن است پس هم زوج و هم فرد است.
- چند خاصیت از توابع زوج و فرد:
- اگر f و g دو تابع زوج باشند آنگاه ترکیبشان یعنی fog(یا gof) هم زوج است.
برهان: باید نشان دهیم:
چون f و g دو تابع زوج هستند طبق فرض داریم:
پس:
لذا تابع fog زوج است به همین روش می توان نشان داد gof هم زوج است.
- اگر f و g دو تابع فرد باشند آنگاه ترکیبشان یعنی fog(یا gof) هم تابعی فرد است.
برهان: باید نشان دهیم:
چون f و g دو تابع فرد هستند داریم:
پس:
لذا تابع fog تابعی فرد است. به همین روش می توان اثبات نمود gof هم تابعی فرد است.
- ترکیب دو تابع که یکی زوج و دیگری فرد باشد همواره تابعی زوج است.
برهان: فرض می کنیم f تابعی زوج دلخواه و g تابعی فرد دلخواه باشد. نشان می دهیم تابع حاصل از ترکیب این دو تابع تابعی فرد است.
طبق فرض داریم:
ابتدا نشان می دهیم تابع fog تابعی فرد است.
پس fog تابعی زوج است. حال نشان می دهیم که gof هم زوج است.
پس gof تابعی زوج است. لذا حکم برقرار است.
- اگر f و g تابعی زوج باشند آنگاه توابع حاصل از اعمال جبری این دو تابع یعنی:
هم توابعی زوج هستند.(در هر حالت می توان جای fو g را با هم عوض نمود)
(البته در مورد تقسیم دو تابع باید در نظر داشت که حکم فوق همواره کلی نمی باشد و به دامنه مخرج بستگی دارد، چرا که ممکن است شرط متقارن بودن تابع حاصل از تقسیم برقرار نباشد.)
برهان: برای نمونه یک حالت زوج بودن را اثبات می کنیم. سایر حالات به طریقی مشابه اثبات می شوند. چون f و g دو تابع زوج هستند داریم:
پس:
لذا تابع f+g تابعی زوج است.
- اگر f و g دو تابع فرد باشند آنگاه تابع تابعی فرد و سایر حالات یعنی: توابعی زوج هستند.
(در هر حالت می توان جای f و g را عوض کرد)
(البته در مورد تقسیم دو تابع باید در نظر داشت که حکم فوق همواره کلی نمی باشد و به دامنه مخرج بستگی دارد، چرا که ممکن است شرط متقارن بودن تابع حاصل از تقسیم برقرار نباشد.)
برهان: ابتدا نشان می دهیم تابعی فرد است. چون دو تابع f و g توابعی فرد هستند داریم:
پس:
لذا دو تابع مذکور فرد می باشند.
حال نشان می دهیم دو تابع زوج می باشند.
(اثبات فوق در باره تقسیم دو تابع با فرض مساعد بودن دامنه f/g برای زوج و فرد بودن نوشته شده است)
پس دو تابع مذکور زوج می باشند.
- اگر f تابعی زوج و g تابعی فرد باشد آنگاه تابعی نه زوج و نه فرد بوده و توابع توابعی فرد می باشند.
برهان: ابتدا به بررسی تابع پردازیم. چون f زوج و g فرد است داریم:
پس:
پس دو تابع فوق در شرایط تابع زوج یا فرد صدق نمی کنند لذا نه زوج و نه فرد هستند.
حال نشان می دهیم در تابع فرد هستند:
(اثبات فوق در باره تقسیم دو تابع با فرض مساعد بودن دامنه f/g برای زوج و فرد بودن نوشته شده است)
پس دو تابع فوق فرد می باشند.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 توابع متناوب
توابع متناوب
توابع متناوب
توابعی را که در طول زمان تکرار میشوند، توابع متناوب میگویند. این منحنی ها به صورت موج سینوسی یا کسینوسی هستند یعنی میتوانند در فواصل زمانی معین تکرار گردند. به صورت نادقیق تابعی از اعداد حقیقی متناوب نامیده میشود، هرگاه مقادیر آن در فواصل معین تکرار شوند.
تابعمتناوب است اگر عددی حقیقی و غیر صفر مانند m باشد بطوری که:
- برای هر از دامنه ی ، عنصر نیز عضوی از دامنه ی باشد.
- برای هر از دامنه، شرط برقرار باشد.
در این تعریف یک دوره ی تناوب تابع متناوب نامیده می شود.
با توجه به رابطه 1 در تعریف فوق ، به سادگی دیده میشود که دامنه تعریف هر تابع متناوب باید بیکران باشد. به عبارت دیگر همه توابعی که دارای دامنه محدود هستند نامتناوب میباشند.
دوره تناوب اصلی
در تابع متناوب عدد حقیقی غیر صفر که برای هر از دامنه تابع، در شرط صدق کند یک دوره تناوب تابع، و کوچکترین مقدار مثبت (در صورت وجود) دوره تناوب اصلی نامیده میشود.
نکته: با توجه به دو تعریف بالا به روشنی دیده میشود که هر مضرب صحیح غیر صفر از هر دوره تناوب یک تابع متناوب نیز میتواند دوره تناوبی از آن تابع باشد.
مثالهایی از توابع متناوب
- در تابع هر عدد صحیح غیر صفر یک دوره تناوب و عدد 1 دوره تناوب اصلی میباشد.
- تابع که در آن عدد حقیقی ثابت میباشد، دارای دوره تناوب اصلی نیست ولی هر عدد حقیقی غیر صفر میتواند دوره تناوب آن باشد.
- تابع را که توسط اگر گویا باشد و اگر اصم باشد، در نظر میگیریم. به ازای هر عدد حقیقی و هر عدد گویای داریم: بنابراین f متناوب، و هر عدد گویا یک دوره تناوب آن میباشد.
ویژگیهای توابع متناوب
- اگر تابع متناوب باشد، برای هر حقیقی غیر صفر، توابع و نیز متناوب خواهند بود و در صورتی که تابع دارای دوره تناوب اصلی برابر با باشد، توابع و دارای دوره های تناوب اصلی به ترتیب برابربا و خواهند بود.
- اگر تابع متناوب باشد، آنگاه برای هر و صحیح غیر صفر، توابع و نیز متناوب خواهند بود.
- اگر تابعی متناوب با دوره تناوب باشد، آنگاه به ازای هر عدد حقیقی و هر عدد صحیح داریم:
از این رو مقادیرد یک تابع متناوب با دوره تناوب، روی هر فاصله با طول تکرار میگردند. نتیجه: اگر تابعی متناوب با دوره تناوب باشد، آنگاه متناوب با دوره تناوب به ازای هر عدد صحیح و غیر صفر نیز هست.
- دوره تناوب اصلی توابع سینوس و کسینوس مساوی با است.
متناوب با دوره تناوب هستند.
- دوره تناوب اصلی هر یک از توابع و برابر و دوره تناوب اصلی هر یک از توابع و برابر است.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |
|
کاربران در حال دیدن موضوع: 1 نفر (0 عضو و 1 مهمان)
|
|
|
 مجوز های ارسال و ویرایش
مجوز های ارسال و ویرایش
|
شما نمیتوانید موضوع جدیدی ارسال کنید
شما امکان ارسال پاسخ را ندارید
شما نمیتوانید فایل پیوست در پست خود ضمیمه کنید
شما نمیتوانید پست های خود را ویرایش کنید
اچ تی ام ال غیر فعال می باشد
|
|
|
اکنون ساعت 04:43 AM برپایه ساعت جهانی (GMT - گرینویچ) +3.5 می باشد.
|










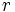
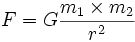

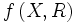
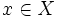
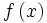
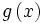
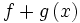
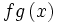
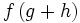
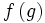
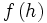
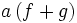
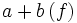
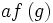
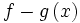
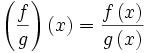
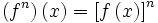
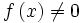
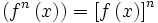
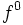
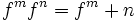
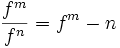
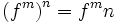
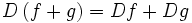

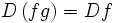
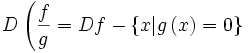
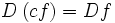
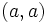
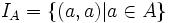
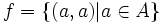
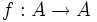
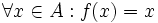
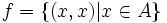
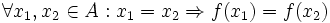
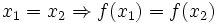
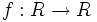

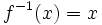
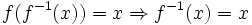
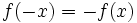
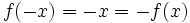
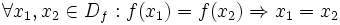
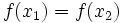
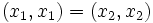
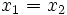
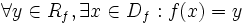
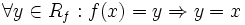
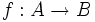
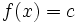

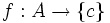
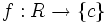
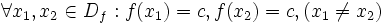
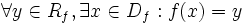
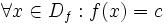
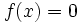
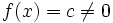
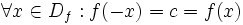
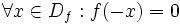
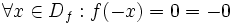
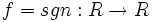
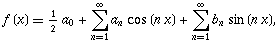
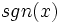
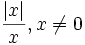
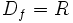
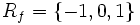
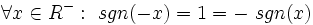
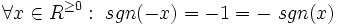
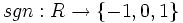
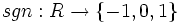
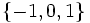
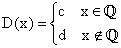
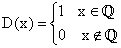
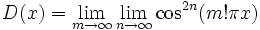
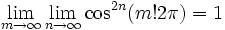
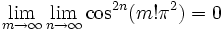
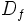
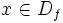
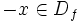
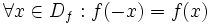
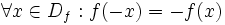
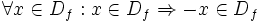
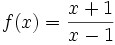
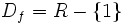
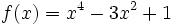
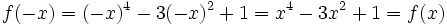
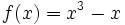
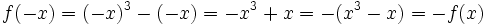
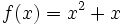
 البته شرط اولیه یعنی متقارن بودن دامنه برقرار است)
البته شرط اولیه یعنی متقارن بودن دامنه برقرار است) 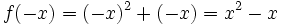
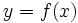
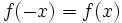

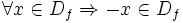
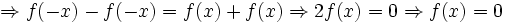
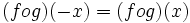
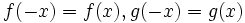
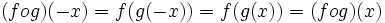
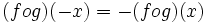
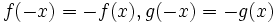
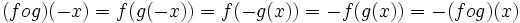
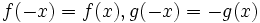
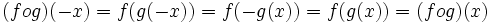
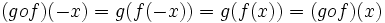
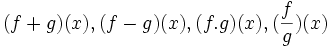
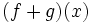
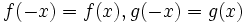
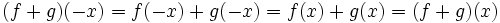
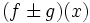
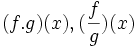
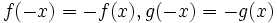
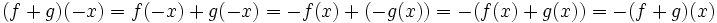
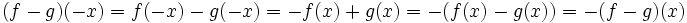
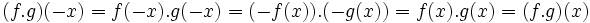
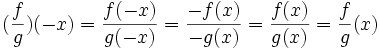
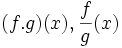
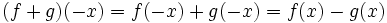
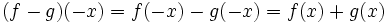
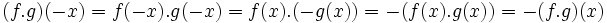


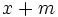
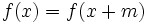
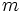
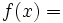
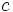
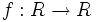
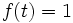
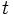
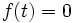
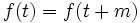
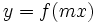

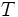
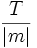

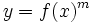
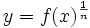
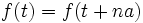
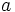
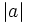

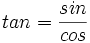
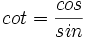
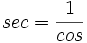
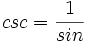
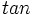
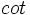
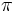
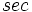
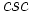
 حالت خطی
حالت خطی

