| فنی و مهندسی در این زیر تالار به بحث و گفتگو در مورد رشته های فنی و مهندسی پرداخته میشود |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 حساب دیفرانسیل و انتگرال
حساب دیفرانسیل و انتگرال
حساب دیفرانسیل و انتگرال
- تاریخچه
- قلمرو امروزی حساب دیفرانسیل و انتگرال
- بزرگان این علم
حسابیا حساب دیفرانسیل و انتگرال ریاضیات مربوط به حرکت و تغییر است.
تاریخچه
حساب دیفرانسیل و انتگرال در آغاز برای براورده کردن نیازهای دانشمندان قرن 17 ابداع شد.البته لازم به ذکر است ریشه های این علمرا میتوان تا هندسه کلاسیک یونانی میتوان ردیابی کرد
حساب دیفرانسیل و انتگرال به دانشمندان امکان می داد شیب خمها را تعریف کنند، زاویه آتشباری توپ را برای حصول بیشترین برد بدست آورند،و زمانهایی که سیارات نزدیکترین و دورترین فاصله را از هم دارند،پیش بینی کنند.
پیش از پیشرفتهای ریاضی که به کشف بزرگ آیزاک نیوتن و لایب نیتس انجامید،یوهانس کپلر منجم با بیست سال تفکر،ثبت اطلاعات،و انجام محاسباث سه قانون حرکت سیارات را کشف کرد:
قانون اول کپلر
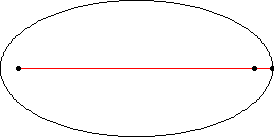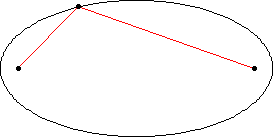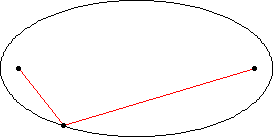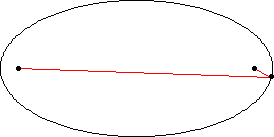
1.هر سیاره در مداری بیضی شکل حرکث میکندکه یک کانونش در خورشید است
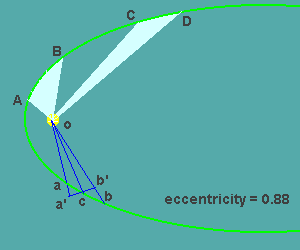
2.خط واصل بین خورشید و ستاره در مدتهای مساوی مساحات مساوی را طی میکنند
قانون دوم کپلر
3.مربع گردش هر سیاره به دور خورشید،متناسب است با مکعب فاصله متوسط آن سیاره از خورشید
ولی استنتاج قوانین کپلر از قوانین حرکت نیوتن با استفاده از حساب دیفرانسیل و انتگرال کار ساده ای است.
قلمرو امروزی حساب دیفرانسیل و انتگرال
امروز حساب دیفرانسیل و انتگرال در آنالیز ریاضی قلمرو واقعا گسترده ای دارد و فیزیکدانان و ریاضیدانان که اول بار این موضوع را ابداع کردند مسلما شگفت زده و شادمان می شدند اگر می دیدند که این موضوع چه انبوهی از مسائل را حل میکند.
امروزه اقتصاددانان از حساب دیفرانسیل و انتگرال برای پیش بینی گرایشهای کلی اقتصادی استفاده می کنند. اقیانوس شناسان برای فرمول بندی نظریه هایی درباره جریانهای دریایی بهره میگیرند،و هواشناسان آن را برای توصیف جریان هوای جو به کار میگیرند،دانشمندان علوم فضایی آن را برای طراحی موشکها به کار میبرند.روانشناسان از آن برای درک ثوهمات بصری استفاده می کنندو...
به طور خلاصه حساب دیفرانسیل و انتگرال علمی است که درتمام علوم امروزی کاربرد بسزایی دارد.
بزرگان این علم
این علم عمدتا کار دانشمندان قرن هفدهم اسث. از میان این دانشمندان میتوان به رنه دکات ،کاوالیری،فرما
و جیمز گرگوری اشاره کرد.
پیشرفت حساب دیفرانسیل و انتگرال در قرن 18 با سرعت زیادی ادامه یافت، در زمره مهمترین افرادی که در این زمینه سهم داشتند میتوان به برادران برنولی اشاره کرد.در واقع خانواده برنولی همان نقشی را در ریاضیات داشتند که خانواده باخ در موسیقی ایفا کردند.
تکمیل ساختار منطقی روشهای حساب دیفرانسیل و انتگرال را ریاضیدانان قرن 19 از جمله لوئی کوشی و کارل وایرشتراس
بر عهده گرفتند.
مطلب را با سخنی از جان فون نویمان که از ریاضیدانان بزرگ قرن بیستم است به پایان میبریم « حساب دیفرانسیل و انتگرال نخستین دستاورد ریاضیات نوین است و درک اهمیت آن کار آسانی نیست. به عقیده من،این حساب روشنتر از هر مبحث دیگری مرحله آغازی ریاضیات نوین را توصیف می کند؛و نظام آنالیز ریاضی، که توسیع منطقی آن است،هنوز بزرگترین پیشرفت فنی در تفکر دقیق به شمار می آید.»
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |
|
جای تبلیغات شما اینجا خالیست با ما تماس بگیرید
|
|

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 حساب برداری
حساب برداری
حساب برداری
حساب برداری، شاخه ای از ریاضیات است که بردارهای چند متغیره را در فضاهای چند بعدی مورد بررسی قرار می دهد و شامل فرمولها و روش های حل مساله زیادی است که در مهندسی و فیزیک کاربر فراوان دارد .
بحث ما درباره بردارها و ارتباط یک بردار با زمینه های اسکالر آن و نیز عکس آن است. به عنوان مثال دمای یک استخر نشان دهنده یک کمیت عددی (اسکالر) است و هر نقطه ای از آب درون آن، دارای یک درجه حرارت است ولی آب جاری درون استخر را می توانیم یک فضای برداری در نظر گرفته و هر نقطه ای از آن را با یک بردار سرعت نشان دهیم. سه عملکرد زیر مهمترین اجزاء حساب برداری هستند:
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 کاربرد مشتق در ترسیم توابع
کاربرد مشتق در ترسیم توابع
کاربرد مشتق در ترسیم توابع
مقدمه
مطالعات ما در مورد مشتق فواید بسیاری دارد از جمله آنها ترسیم توابع است. برای تعیین شکل نمودار از مشتقهای اول و دوم تابع استفاده میکنیم. مشتق اول تعیین میکند که نمودار در کجا صعودی و در کجا نزولی است. مشتق دوم ما را مطلع میسازد که تقعر نمودار کجا رو به پایین و کجا رو به بالا است. بسیاری از نمودارهای وقتی X بزرگ شود، یا به مقادیر خاصی میل کند به خط مستقیم میل میکنند که تمام این مطالب بررسی خواهد شد.
رسم خم با استفاده از مشتق اول
وقتی بدانیم که تابعی در هر نقطه از بازهای مشتق دارد، بنابر قضایای مشتق خواهیم دانست که تابع در سراسر آن بازه پیوسته است و نمودارش در آن بازه قطع شدگی ندارد. مثلا نمودارهای توابع مشتقپذیر y=Sin x همانند نمودار چند جملهایها ، هر چه ادامه بیابند قطع نمیشوند. نمودارهای y = tan x و y = 1/x2 صرفا در نقاطی که توابع مربوط تعریف نشده هستند قطع میشوند. بر بازهای که این نقاط را شامل نباشند توابع مزبور مشتق پذیرند؛ و بنابراین پیوستهاند و نمودارهایشان قطع شدگی ندارد. اگر بدانیم مشتق تابعی کجا مثبت و کجا منفی و کجا صفر میباشد، آنگاه میتوانیم درباره شکل نمودار آن تابع اطلاعاتی بدست آوریم. با دانستن این مطلب میتوان مشخص کرد که نمودار در کجا بالا میرود ، پایین میآید یا مماس افقی دارد.
تایعی چون (y = f(x را سراسر یک بازه I صعودی میگویند. هرگاه با افزایش y , x هم زیاد شود ؛ و در سراسر I نزولی گویند هرگاه با افزایش x و y کاهش یابد. وقتی x در I از چپ به راست حرکت میکند نمودار یک تابع صعودی ، خیز بر میدارد و نمودار یک تابع نزولی افت میکند. صعود یک تابع با مشتقهای مثبت همراه است و نزول تابع با مشتقهای منفی. بنابراین اگر ´f در هر نقطه از یک بازه I مثبت لاشد آنگاه f بر I صعود می کند. و اگر ´f در هر نقطه I منفی باشد، آنگاه f بر I نزول میکند. این واقعیتها را به عنوان آزمون مشتق اول برای صعودی و نزولی بودن میپذیریم. آزمون مشتق اول به زبان هندسی حاکمی است که توابع مشتقپذیر بر بازههایی صعود میکنند که نمودارشان شیب مثبت داشته باشند و بر بازههایی نزول می کنند که نمودارشان شیب منفی داشته باشند.
مماسهای افقی
از آنجا که مشتقی چون ´f در هر بازه I یی که َf تعریف شود دارای ویژگی مقدار میانی است، هر وقت ´f در این بازه تغییر علامت میدهد، باید مقدارش صفر شود. پس هر وقت َf در بازه I تغییر علامت میدهد نمودار f باید مماس افقی داشته باشد. اگر وقتی x از چپ به راست میرود و از نقطهای چون C میگذرد، مقدار ´f از مثبت به منفی تبدیل شود، آنگاه مقدار f در c یک مقدار Max موضعی f است. به همین ترتیب اگر وقتی x از از چپ به راست حرکت میکند و از نقطهای چون d میگذرد. مقدار ´f از منفی به مثبت تبدیل شود. مقدار f در d یک مقدار Min موضعی f است. *نمیتوان گفت که هر وقت مشتق صفر شد الزاما تغییر علامت در نمودار تابع ایجاد میشود، بنابراین گاهی اوقات در حالی که Min , Max وجود ندارند مماس افقی وجود دارد، مثل تابع y = x3 با اینکه y´= 3x2 در مبدأ صفر است و در هر دو طرف مثبت است. با این همه مماس افقی y=0 نمودار y = x3 را در مبدأ قطع میکند.
تقعر و نقطه عطف
در این قسمت چگونگی رسم دقیقتر نمودار با استفاده از علامت مشتق دوم تابع را تشریح میکنیم. همان طور که میدانیم تابع y = x3 (برای خودتان رسم کنید) همراه با افزایش x صعود میکند. اما قسمتی از خم که مربوط به بازه (0, ∞-) و قسمت مربوط به (∞و0) در جهتهای متنفاوتی میپیچیند، اگر در امتداد خم از سمت چپ به طرف مبدأ برویم پیچش خم به سمت راست است. وقتی از مبدأ دور میشویم، خم به سمت چپ میپیچد. توصیف پیچش به طریق دیگر این است که وقتی نقطه تماس از سمت چپ به مبدأ میل میکند مماس بر خم در جهت ساعت میچرخد، در این حالت شیب خم تقلیل مییابد. وقتی نقطه تماس از مبدأ وارد ربع اول میشود، مماس در خلاف جهت ساعت میچرخد. در این حالت میگوییم شیب خم زیاد شده است. بنابراین برای یافتن روی تقعر توسط مشتق باید بگوییم در بازهای که ´y کم میشود تقعر رو به پایین دارد و در بازهای که ´y زیاد میشود تقعر رو به بالا دارد. توسط آزمون مشتق دوم میتوانیم بگوییم در نمودار (y = f(x ، در بازهای که مشتق دوم y کوچکتر از صفر باشد، تقعر رو به پایین دارد. در بازه ای که مشتق دوم y بزرگتر از صفر باشد، تقعر رو به بالا دارد.
کاربرد نقطه عطف در رسم توابع
نقطهای از خم که در آن تقعر عوض میشود نقطه عطف داریم. پس نقطه عطف خمی که دو بار مشتق پذیر است نقطهای است در یک طرفش مثبت و در طرف دیگرش منفی است و خود مشتق دوم y در نقطه عطف مقدار صفر دارد. البته ممکن است مشتق دوم y در نقطهای که عطف نیست صفر باشد. همچنین ممکن است نقطه عطف در جایی باشد که مشتق دوم y وجود نداشته باشد.
مجانبها و تقارن
در این قسمت توابع گویا از x را با در نظر گرفتن رفتارشان ، وقتی مخرج به صفر نزدیک یا x از لحاظ عددی بزرگ میشود، بررسی می کنیم. نمودار تابعهای زوج و فرد تقارنهایی دارند که آگاهی از آنها برای ترسیم نمودارشان مفید و مهم است.
- باید این را بدانیم که نمودار توابع زوج نسبت به محور yها متقارن است و نمودار توابع فرد نسبت به مبدأ مختصات متقارن میباشد.
مجانبهای افقی و قائم
وقتی یک نقطه p روی نمودار تابعی چون (y = f(x رفته رفته از مبدأ دور میشود، ممکن است فاصله بین p و خطی ثابت به صفر نزدیک شود؛ به عبارت دیگر ، خم وقتی از مبدأ دور میشود به خط میل کند. در این حالت ، خط را مجانب نمودار مینامند.
خط y = b مجانب افقی نمودار (y = f(x است اگر داشته باشیم: حد تابع (y = f(x وقتی که x به سمت بینهایت و یا منفی بینهایت میل میکند برابر با b شود.
خط x = a مجانب قائم نمودار تابع است، اگر داشته باشیم: حد تابع (y = f(x وقتی که x به سمت a- و یا a+ میل میکند برابر با ∞± شود.
مجانب مایل
اگر تابع گویایی خارج قسمت دو چند جملهای باشد که عامل مشترک نداشته باشند و اگر درجه صورت ، یک واحد از درجه مخرج بیشتر باشد، آنگاه نمودار یک مجانب مایل دارد. و بطور کلی برای رسم نمودار یک تابع باید مجانبها ، تقعرها ، نقاط عطف ، مماسها ، نقاط اکسترمم باید مشخص باشند.
کاربردها
رسم توابع مورد بحث ما در جاهای بسیار وسیع کاربرد دارد. برای مثال پرتاب یک موشک یا یک سفینه با بدست آوردن توابع مربوط و رسم نمودار آ«ها توسط کامپیوتر قبل از عملیات پرتاب توسط مهندسین مورد بررسی قرار میگیرد تا نحوه حرکت و سایر موارد مو شکافی گردد. در ستاره شناسی ، مکانیک ، شیمی و حتی علوم انسانی رسم نمودار توابع از ارزش اجتناب ناپذیری برخوردار است.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 توابع صعودی و نزولی
توابع صعودی و نزولی
توابع صعودی و نزولی
تابع f را روی بازه I صعودی اکیدا صعودی نامند، اگر برای هر x1 و x2 عضو I که x1 > x2 داشته باشیم: (f(x1) ≤ f(x2. تابع f را روی بازه I نزولی (اکیدا نزولی) گوئیم اگر برای x1 و x2 عضو I که x1 > x2 تابعی مانند (f(x2) ≤ f(x1 داشته باشیم.
تشخیص توابع اکیدا یکنو از روی شکل تابع
- نمودار تابع پیوسته f را وقتی صعودی اکیدا گوئیم که اگر از سمت چپ شکل روی نمودار حرکت کنیم، همواره به طرف بالا برویم.
- نمودار تابع پیوسته f را وقتی نزولی اکید گوئیم که اگر از سمت چپ شکل روی نمودار حرکت کنیم همواره به طرف پایین برویم.
- نمودار تابع f را وقتی صعودی گوئیم که اگر از سمت چپ شکل روی نمودار حرکت کنیم، به طرف بالا برویم و در قسمتی از نمودار حرکت افقی باشد.
- نمودار تابع پیوسته f را وقتی نزولی گوئیم که اگر از سمت چپ شکل روی نمودار حرکت کنیم به طرف پایین بیائیم و در قسمتی از نمودار ، حرکت افقی باشد.
- تذکر: توابع صعودی یا نزولی را توابع یکنوا مینامند، مثل انباری که بطور یکنواخت به آن گندم میریزند و یا منابعی که بطور یکنواخت کاهش مییابند و بسیاری از پدیدههای اطراف دارای تابع یکنوا میباشند.
رابطه بین مشتق و توابع یکنوا
فرض کنیم که تابع حقیقی f بر بازه بسته (a و b) پیوسته و بر بازه باز (a و b) مشتق پذیر باشد در این صورت:
- اگر برای هر a < x < b داشته باشیم: مشتق اول تابع f بزرگتر از صفر ، آنگاه f اکیدا صعودی است.
- اگر برای هر a < x < b داشته باشیم: مشتق اول تابع f کوچکتر از صفر ، آنگاه f اکیدا نزولی است.
در هر یک از دو قسمت فوق اگر داشته باشیم مشتق اول تابع f بزرگتر یا مساوی صفر یا مشتق اول تابع f کوچکتر یا مساوی صفر. در این صورت حکم قضیهها وقتی برقرار است که تعداد ریشههای معادله 0 = (f'(x متناهی باشد. آزمون مشتق اول به زبان هندسی حاکی است که توابع مشتق پذیر بر بازههایی صعود میکنند که نمودارشان شیب مثبت داشته باشد و بر بازههایی نزول میکنند که نمودارشان شیب منفی داشته باشید.
نکته
برای تعیین فواصل یکنوایی تابع حقیقی F ، باید مشتق تابع را تعیین کنیم. حدول تعیین علامت مشتق را جدول تغییرات نمودار تابع F میگویند. همچنین نقطهای به طول X=C را از دامنه تابع F را نقطه اکسترمم نسبی F میگویند، هرگاه مشتق در این نقطه ، تغییر علامت دهد.
چشم انداز بحث
با توجه به روابط ذکر شده و تعیین رابطه آهنگهای تغییر مثلا تعیین کنیم که دو کشتی با چه سرعتی از هم دور میشوند یا وقتی حباب صابون باد میکند شعاع آن با چه سرعتی زیادتر میشود.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 مشتق
مشتق
مشتق
- مشتق گیری و مشتق پذیری
- بررسی مشتق از نظر هندسی
- ارتباط مشتق با علم فیزیک
- نقاط بحرانی
- تجزیه و تحلیل نمودارها
- همچنین ببینید:
- منابع خارجی
مشتق یکی از مهمترین مفاهیم ریاضی است. بوسیله مشتق میتوان برخی از مفاهیم فیزیکی (مانند سرعت و شتاب)با تعاریف ریاضی بیان نمود.
ااگر منحنی یک تابع را در فضای دو بعدی در نظر بگیریم بوسیله مشتق میتوانیم شیب خط مماس بر منحنی را در هر نقطه دلخواه بدست آوریم.همچنین با استفاده از مشتق میتوان خواص هندسی منحنی یک تابع مانند تقعر و تحدب را مشخص کرد.
البته باید به این نکته توجه کرد که هر تابعی در هر نقطه نمیتواند مشتق داشته باشد و به طور کلی مشتق پذیری یک تابع در یک نقطه شرایط خاصی میطلبد.
مشتق گیری و مشتق پذیری
در گذشته های نه چندان دور، مشتق یک تابع را به صورت زیر نشان می دادند:
که در این فرمولنشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند:
معمولا از نمادهای زیر برای نشان دادن مشتق تابع f نسبت به متغیر x، استفاده میکنند:
یک تابع را در نقطه ای مانند x مشتق پذیر گویند اگردر آن نقطه مشتق موجود باشد. و برای مشتق پذیری تابع در یک بازه لازم است تابع در هر نقطه دلخواه از بازه مشتق پذیر باشد.اگر تابع در نقطه ای مانند c پیوسته نباشد آنگاه در c نمیتواند مشتق پذیر باشد.البته لازم به ذکر است که پیوستگی در یک نقطه وجود مشتق را تضمین نمیکند.مشتق یک تابع مشتق پذیر میتواند خود نیز مشتق پذیر باشد،که به مشتق آن مشتق دوم تابع گویند.مشتق مراتب بالاتر نیز به همین ترتیب تعریف میشوند.
بررسی مشتق از نظر هندسی
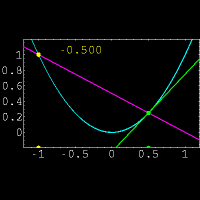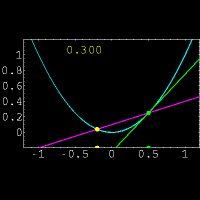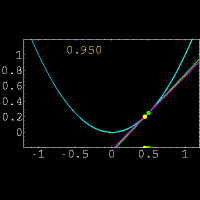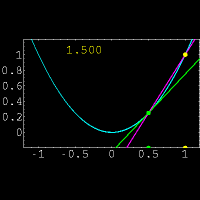
از نظر هندسی مشتق یک تابع در یک نقطه دلخواه ،شیب خط مماس بر منحنی در آن نقطه است.البته پیدا کردن مستقیم شیب خط مماس در یک نقطه کار دشواری است.زیرا فقط مختصات یک نقطه از خط مماس را داریم.(برای پیدا کردن شیب یک خط از مختصات دو نقطه بر روی خط استفاده میکنیم)برای حل این مشکل از یک خط متقاطع استفاده کرده و این خط را به خط مماس نزدیک میکنیم.برای درک بهتر موضوع به شکل مقابل توجه نمایید.در این شکل خط متقاطع با رنگ بنفش و خط مماس با رنگ سبز مشخص شده است و عددی که در تصویر تغییر میکند نشان دهنده شیب خط متقاطع میباشد. حال از دیدگاه ریاضی این روش را بیان میکنیم:
از دیدگاه ریاضی بدست آوردن مشتق با حدگیری از شیب خط قاطع که به خط مماس نزدیک شده است بدست می آید.پیدا کردن شیب نزدیکترین خط متقاطع به خط مماس با استفاده از کوچکترین h در فرمول زیر حاصل میشود:
عکس پیدا نشد بزرگنمایی خط مماس بر یک نقطه روی خط
در این فرمول h به عنوان کوچکترین تغییر متغیر x تعریف میشودو میتواند مقدار مثبت یا منفی اختیار کند. در این فرمول شیب خط با استفاده از نقاط و حاصل میشود.واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش مشتق x ،حاصل حد زیر است:
ارتباط مشتق با علم فیزیک
مشتق نقش مهمی در تعریف برخی ار کمیتهای فیزیک حرکت دارد.ما با داشتن موقعیت اجسام بر حسب زمان میتوانیم سرعت و شتاب آنها را محاسبه کنیم.اگر ما از معادله مکان جسم بر حسب زمان مشتق بگیریم معادله سرعت بدست میآید و اگر از معادله سرعت مشتق گیری نماییم(مشتق دوم معادله مکان)معادله شتاب حاصل میشود.
نقاط بحرانی
نقاطی از تابع که به ازای آنها مشتق تابع تعریف نشده و یا برابر صفر باشد را نقاط بحرانی مینامند.اگر مشتق دوم در یک نقطه بحرانی مثبت باشد،آن نقطه مینیمم نسبی است.و اگر منفی باشدماکزیمم نسبی است،و اگر برابر صفر باشد ممکن است ماکزیمم و مینیمم نسبی نباشد.مشتق گرفتن و بدست آوردن نقاط بحرانی،اغلب ساده ترین راه برای پیدا کردن مینیمم و ماکزیمم نسبی است.(در بهینه سازی نیز این روش بسیار مفید است.به طور کلی مینیمم و ماکزیمم نسبی فقط میتوانند جزئ نقاط بحرانی باشند.
تجزیه و تحلیل نمودارها
مشتق ابزار مناسبی برای آزمودن نمودار تابع است. نقاطی از دامنه تابع که به ازای آنها مشتق اول برابر صفر شود میتوانند نقاط اکسترمم نسبی تابع باشند.البته باید توجه کرد که تمام نقاط بحرانی نقاط اکسترمم نسبی نیستند.برای مثال تابع یک نقطه بحرانی در x=0 دارد، ولی میتوان از نمودار تابع متوجه این نکته شد که تابع در این نقطه دارای ماکزیمم یا مینیمم نسبی نیست.
آزمون مشتق اول و آزمون مشتق دوم ، روش هایی را برای تشخیص نقاط ماکزیمم و مینیمم نسبی فراهم میکند.لازم به ذکر است در فضاهای چند بعدی نقاط اکسترمم را با استفاده از مشتقات جزئی بدست میآورند.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 حد
حد
حد
- حد تابع در یک نقطه
- تعریف مجرد حد:
- حد توابع در بی نهایت
- حد یک دنباله
- پیوند خارجی
در ریاضیات، مفهوم حد، برای بیان رفتار یک تابع مورد استفاده قرار می گیرد و به بررسی این رفتار در نقاط روی صفحه و یا در بی نهایت می پردازد. حد در حساب دیفرانسیل و انتگرال و نیز در آنالیز ریاضی برای تعریف مشتق و نیز مفهوم پیوستگی مورد استفاده قرار می گیرد.
ریاضیدانها حتی قبل از اینکه بتوانند مفهوم دقیق حد را بیان کنند، در مورد آن بحث می کرده اند. یونانیان باستان درکی از مفهوم حد داشته اند. مثلاً ارشمیدس مقدار تقریبی را با استفاده از محیط چند ضلعیهای منتظم محاط در دایره به شعاع واحد، وقتی که تعداد اضلاع بدون کران افزایش می یابد به دست می آورد. در قرون وسطی نیز تا زمان رنسانس انواع مفاهیم حد برای بدست آوردن مساحت شکلهای مختلف به کار رفته است.
نیوتن و لایب نیتسدر قرن هفدهم، درک شهودی خوبی از حد داشته و حتی حدهای پیچیده ای را نیز محاسبه کرده اند. اما نه آنها و نه در آن قرن، دانشمندان دیگر تعریف دقیقی از حد را ارائه نکرده اند.
یک قرن پس از پیشرفت حساب دیفرانسیل و انتگرال، آلمبرت در سال 1754 عنوان کرد که پایه منطقی مباحث این رشته از دانش بشری مفهوم حداست. کوشی در اوایل قرن نوزدهم حساب دیفرانسیل و انتگرال را به شکلی شبیه آنچه در حال حاضر می خوانیم ارائه داد:
"وقتی که مقادیر متوالی به یک متغیر نسبت داده می شود، بی نهایت به عدد ثابتی نزدیک شوند، به طوری که اختلاف آنها از مقدار ثابت به هر اندازه کوچک قابل انتخاب باشد، این مقدار ثابت را حد همه مقادیر متغیر می گویند."
اگر چه تعریف او از حد باز هم دقیق نبود ولی او قدم بزرگی برای رسیدن به تعریف دقیق فعلی برداشت. تا اینکه سرانجام ویراشتراس در قرن نوزدهم تعریف دققی حد را مطرح کرد که همواره مورد استفاده ریاضیدانان است و در این کتاب نیز آورده شده است.
حد تابع در یک نقطه
اگر یک تابع و یک عدد حقیقی باشد و داشته باشیم: آن گاه این فرمول را چنین میخوانیم << حد تابع f وقتی که x به سمت می رود برابر L است>> توجه کنید که این عبارت حتی اگر
باشد نیز می تواند درست باشد. در عوض تابع در نقطه c تعریف نشده است.حالی مثالی را ذکر می کنیم:تابع زیر را در نظر میگیریم
حال متغیر x را به عدد2 نزدیک می کنیم و خواهیم دید که مقدار تابع به 0.4 نزدیک می شود. در این مورد مشاهده می شود که در این صورت گزینه تابع در نقطه X=C دارای
پیوستگی است. اما همیشه این مورد برقرار نیست.
منحنی زرد رنگ در همه جا پیوسته بوده و دارای حد است ولی سه شکل دیگر نمایانگر انواع ناپیوستگی یک نمودار در یک نقطه است
تعریف مجرد حد:
فرض کنید f تابعی باشد روی یک بازه باز که شامل نقطه C است و فرض کنید L یک عدد حقیقی باشد در این صورت را به صورت زیر تعریف میکنیم:
به ازای هروجود دارد یک که برای هر x دلخواه اگر آنگاه نتیجه بگیریم:
حد توابع در بی نهایت
حد یک تابع فقط در نزدیکی اعداد متناهی تعریف نمی شود بلکه ممکن است متغیر توابع وقتی که بی نهایت نزدیک می شود دارای حد باشند.
به عنوان مثال در تابع خواهیم داشت:
- f(100) = 1.9802
- f(1000) = 1.9980
- f(10000) = 1.9998
مشاهده میشود که هر چه قدر x بزرگتر میشود ،مقدار تابع به عدد 2 نزدیکتر میشود .در واقع داریم:
حد یک دنباله
حد یک دنباله مانند 1.79, 1.799, 1.7999,... را در نظر بگیرید. مشاهده می کنیم که این دنباله به عدد 1.8 نزدیک می شود.
به طور کلی فرض می کنیم یک دنباله از اعداد حقیقی باشد. می گوییم حد این دنباله برابر L است و می نویسیم: اگر و تنها اگر برای هر یک عدد طبیعی مانند m باشد که برای هر n>m داشته باشیم
باید توجه کرد که ما می توانیم مقدار . را به عنوان فاصله بین و L در نظر بگیریم به چنین دنباله هایی که حد آنها به یک عدد متناهی میل می کند همگرا گویند و گرنه به آن واگرا گویند.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 پیوستگی
پیوستگی
پیوستگی
توابع پیوسته
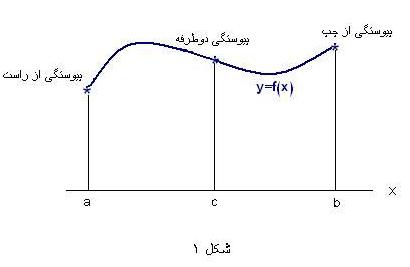
تابعی مانند که بتوان نمودار آن را در هر بازه ای از دامنه اش با حرکت پیوسته نوک قلم رسم کرد مثالی از یک تابع پیوسته است. نمودار این تابع در طول بازه به طور پیوسته با تغییر می کند. در هر نقطه داخلی دامنه تابع مانند نقطه در شکل (1) مقدار تابع حد مقادیر تابع در هر یک از دو طرف است.یعنی :
مقدار تابع در هر یک نقطه انتهایی نیز حد مقادیر تابع در نزدیکی آن است.در نقطه انتهایی چپ :
و در نقطه انتهایی راست :
پیوستگی در یک نقطه داخلی
تابعی چون در یک نقطه داخلی از دامنه اش مانند پیوسته است اگر و فقط اگر :
پیوستگی در یک نقطه انتهایی
تابعی چون در یک نقطه انتهایی چپ از دامنه اش مانند پیوسته است اگر و تنها اگر :
تابعی چون در یک نقطه انتهایی راست از دامنه اش مانند پیوسته است اگر و تنها اگر :
تابع پیوسته به بیان دیگر
یک تابع پیوسته است اگر در هر نقطه از دامنه اش پیوسته باشد.
ناپیوستگی در یک نقطه
اگر تابعی چون در نقطه ای مانند پیوسته نباشد گوییم در ناپیوسته است و را یک نقطه ناپیوستگی می خوانیم.
آزمون پیوستگی
تابع در پیوسته است اگر و تنها اگر هر سه گزاره زیر درست باشد :
الف. وجود دارد. ( در دامنه است.)
ب. وجود دارد. ( وقتی دارای حد است.)
ج. (این حد برابر با مقدار تابع است.)
در آزمون فوق اگر یک نقطه داخلی دامنه باشد حد مورد نظر دوطرفه است و اگر یک نقطه انتهایی دامنه باشد حد مزبور یک حد یک طرفه مناسب (چپ یا راست) است.
قضیه ترکیب حدها برای توابع پیوسته
اگر توابع در پیوسته باشند آنگاه همه ترکیبات زیر در پیوسته اند :
1.
2.
3.
4.
قضیه
هر تابع در هر نقطه ای که مشتق داشته باشد در آن نقطه پیوسته است. یعنی اگر در دارای مشتق باشد آنگاه در پیوسته است.
قضیه
اگر در و در پیوسته باشند آنگاه تابع مرکب در پیوسته است.
قضیه ماکسیمم-مینیمم برای توابع پیوسته
اگر در هر نقطه از بازه بسته پیوسته باشد آنگاه یک مقدار می نیمم و یک مقدار ماکزیمم بر اختیار می کند. یعنی اعدادی چون در وجود دارند به طوری که و و برای هر نقطه مانند در داریم :
قضیه مقدار میانی
اگر در هر نقطه از بازه بسته پیوسته باشد و عددی بین و باشد آنگاه دست کم یک نقطه بین وجود دارد که در آن نقطه مقدار را اختیار می کند. به شکل (2) توجه کنید.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 انتگرال
انتگرال
انتگرال
- محاسبه انتگرال
- تقریب انتگرالهای معین
- تعریف های انتگرال
- سایتهای مرتبط
- پیوندهای خارجی
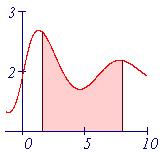
در حساب دیفرانسیل و انتگرال ، از انتگرال یک تابع برای عمومیت دادن به محاسبه مساحت ، حجم ، جرم یک تابع استفاده می شود. فرایند پیدا کردن جواب انتگرال را انتگرال گیری گویند.البته تعاریف متعددی برای انتگرال گیری وجود دارد ولی در هر حال جواب مشابه ای از این تعاریف بدست می آید. انتگرال یک تابع مثبت پیوسته در بازه (a,b) در واقع پیدا کردن مساحت بین خطوط x=0 , x=10 و خم منفی F است . پس انتگرال F بین a و b در واقع مساحت زیر نمودار است. اولین بار لایب نیتس نماد استانداری برای انتگرال معرفی کرد و به عنوان مثال انتگرال f بین a و b رابه صورت نشان می دهند علامت ،انتگرال گیری از تابع f را نشان می دهند ،aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال پذیر است و dx نمادی برای متغیر انتگرال گیری است.
انتگرال یک تابع مساحت زیر نمودار آن تابع است.
از لحاظ تاریخی dx یک کمیت بی نهایت کوچک را نشان می دهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی
پایه گذاری شده است به عنوان مثال تابع f را بین x=0 تا x=10 در نظر بگیرید ،مساحت زیر نمودار در واقع مساحت مستطیل خواهدبود که بین x=0 ،x=10 ،y=0 ،y=3 محصور شده است یعنی دارای طول 10 و عرض 3است پس مساحت آن برابر 30 خواهد بود .
اگر تابعی دارای انتگرال باشد به آن انتگرال پذیر گویند و تابعی که از انتگرال گیری از یک تابع حاصل می شود تابع اولیه گویند . اگر انتگرال گیری از تابع در یک محدوده خاص باشند به آن انتگرال معین گویند که نتیجه آن یک عدد است ولی اگر محدوده آن مشخص نباشد به آن انتگرال نامعین گویند.
محاسبه انتگرال
اکثر روش های اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده است که بر طبق آن داریم:
1.f تابعی در بازه (a,b) در نظر می گیریم .
2.پاد مشتق f را پیدا می کنیم که تابعی است مانند f که و داریم:
3.قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر می گیریم:
بنابراین مقدار انتگرال ما برابر خواهد بود.
به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه می دهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم .
معمولاً پیدا کردن پاد مشتق تابع f کار ساده ای نیست و نیاز به استفاده از تکنیکهای انتگرالگیری دارد این تکنیکها عبارتند از :
- انتگرال گیری بوسیله تغییر متغیر
- انتگرال گیری جزء به جزء
- انتگرال گیری با تغییر متغیر مثلثاتی
- انتگرال گیری بوسیله تجزیه کسرها
روش هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار می رود همچنین می توان بعضی از انتگرال ها با ترفند هایی حل کرد برای مثال می توانید به انتگرال گاوسی مراجعه کنید .
تقریب انتگرالهای معین
محاسبه سطح زیر نمودار بوسیله مستطیل هایی زیر نمودار.
هر چه قدرعرض مستطیل ها کوچک میشوندمقدار دقیق تری
از مقدار انتگرال بدست میآید.
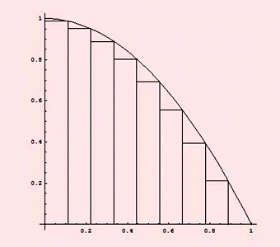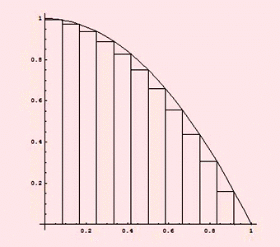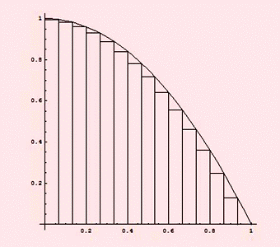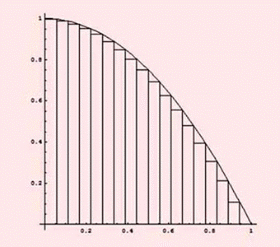
انتگرال هایی معین ممکن است با استفاده از روش های انتگرال گیری عددی ،تخمین زده شوند.یکی از عمومی ترین روش ها ،روش مستطیلی نامیده می شود در این روش ناحیه زیر نمودار تابع به یک سری مستطیل تبدیل شده و جمع مساحت آنها نشان دهنده مقدار تقریبی انتگرال است.
از دیگر روش هایی معروف برای تخمین مقدار انتگرال روش سیمپسون و روش ذوزنقه ای است. اگر چه روش های عددی مقدار دقیق انتگرال را به ما نمی دهند ولی در بعضی از مواقع که انتگرال تابعی قابل حل نیست یا حل آن مشکل است کمک زیادی به ما می کند .
تعریف های انتگرال
از مهم ترین تعاریف در انتگرال می توان از انتگرال ریمان و انتگرال لبسکی(lebesgue) است. انتگرال ریمان بوسیله برنهارد ریمان در سال 1854 ارئه شد که تعریف دقیقی را از انتگرال ارائه می داد تعریف دیگر را هنری لبسکی ارائه داد که طبق این تعریف شرایط تعویض پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه می کرد.
از دیگر تعاریف ارائه شده در زمینه انتگرال میتوان به انتگرال riemann-stieltjes اشاره کرد. پس به طور خلاصه سه تعریف زیر از مهمترین تعاریف انتگرال میباشند:
- انتگرال ریمان
- انتگرال لبسکی
- انتگرال riemann-stieltjes
- انتگرالهای چند گانه
- روشهای انتگرال گیری
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 انتگرال ریمان
انتگرال ریمان
انتگرال ریمان
- مجموع ریمان :
- انتگرال ریمان:
- همچنین ببینید:
پیدا کردن مساحت
هاشور خورده
همان طور که می توانیم پیدا کردن مساحت زیر یک نمودار منحنی، کار ساده ای نیست. چونسطح زیر منحنی یک شکل منظم نیست پس هیچ فرمول تعریف شده ای برای پیدا کردن مساحت آن وجود ندارد. بنابراین ما به دنبال راهی برای حل این مشکل هستیم.
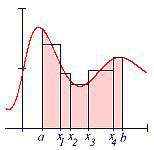
حال به دنبال راهی برای تخمین مساحت زیر منحنی هستیم.یکی از این راهها استفاده از مجموعه ای از مستطیلها است. ابتدا بازه به چندین جزء بوسیله انتخاب چهار نقطه تا روی محور xها تقسیم می کنیم. و عرض مستطیل ها را بر این نقاط بنا می کنیم.(همانند شکل) با جمع مساحت مستطیل ها می توان مساحت زیر نمودار را تخمین زد.
برای محاسبه ارتفاع مستطیل ها، نقطه ای مانند را انتخاب می کنیم. ارتفاع ما به نزدیک خواهد بود.
ولی این ارتفاع دقیق نیست. بنابراین نقطه ای مانند بین های متوالی انتخاب می کنیم. در این حالت مقدار دقیق تری را اختیار می کند. اگر
تعریف کنیم در این صورت جمع مساحت مستطیل ها برابر خواهد بود با
مجموع ریمان:
مجموع مساحت مستطیل های که ما برای تخمین مساحت زیر منحنی استفاده می کنیم. مجموع ریمان نامیده می شود. حال با مثالی این مجموع را توضیح می دهیم:
تابع:
نقاط شروع و پایان بازه:
تعداد مستطیل ها (یا تعداد بازه ها) :
با استفاده از مجموع ریمان:
خواهیم داشت:
11.924959 =مقدار دقیق مساحت
11.8740138= مساحت محاسبه شده
بین مجموع ریمان و مقدار دقیق جواب اگر مقایسه ای انجام دهید
در این صورت مقدار خطای با برابر خواهد بود با:
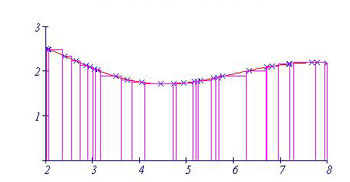
همانطور که مشاهده شد مستطیل ها به صورت رندومی تولید شده اند و تعداد آنها محدود است. حال به نظر شما اگر تعداد مستطیلها یعنی nرا افزایش دهیم و مستطیل ها، حالت منظم به خود بگیرند چه اتفاقی خواهد افتاد.البته توجه کنید که nهای مختلف، مجموع ریمان مختلفی تولید می کنند.
مثال :
می خواهیم مجموع ریمان برای مساحت زیر نمودار منحنی دربازه را پیدا کنیم
1) بازه را به 5 قسمت، از تا تقسیم می کنیم:
2) عرض مستطیل ها را پیدا می کنیم.
تا
3) نقاط را در بین ها برای پیدا کردم ارتفاع مستطیل که برابر با خواهد بود، قرار می دهیم در این صورت:
تا
4) پیدا کردن مساحت 5 مستطیل:
تا را پیدا میکنیم.
5) مساحت های بدست آمده را با هم جمع می کنیم:
انتگرال ریمان:
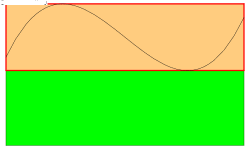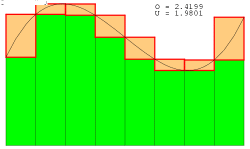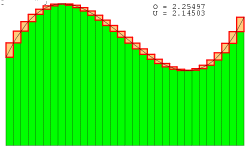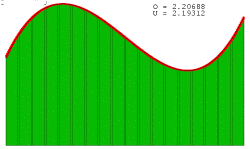
این شکل همگرایی مجموع ریمان
را نشان میدهدهر چه قدر بازه ها کوچکتر
و تعداد مستطیلها بیشتر میشود
مقدار O(حد مجموع بالا)و U (حد مجموع پایین)
به مقدار اصلی مساحت نزدیک خواهد شد.
ممکن است تا اینجا به این نکته رسیده اید که هر چه قدرعددn (یعنی تعداد مستطیلها) بیشتر باشد مجموع ریمان به یک عدد ،همگرا میشود. یعنی حد گرفتن از مجموع ریمان وقتی که n بسیار بزرگ است مساحت زیر نمودار را به ما می دهد.
تعریف انتگرال ریمان:
اگر f تابعی باشد که دربازه تعریف شده است در این صورت مجموع ریمان تابعf در بازه وقتی که n به سمت بی نهایت می رود،همگرا به یک مقدار محدود مانند Aخواهد بود.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 ریمان
ریمان
ریمان
گیورک فریدریش بر نهارد ریمان (1826-1866 میلادی) مقارن ولد هندسه نااقلیدسی قدم به عرصه وجود گذاشت. پس از تحصیلات مقدماتی و متوسطه به عزم علوم الهی به دانشگاه گوتینگن روی آورد اما زود دریافت که که آنچه با مذاق وی سازگاری داشت ریاضیات بود نه الهیات ریمان یی از برجسته ترین شاگردان گوس شمرده می شود بعدا به برلن رفت و در محضر استادان دیگری تلمذ کرد و در سال 1840 به گوتینگن بازگشت و در رشته فیزیک درجه علمی رفت.
زریمان در سال 1854 رساله ای تنظیم کرد و در آن خاطرنشان ساخت که هر چند جهان نامحدود است، بی پایان
رفتن آن ضرور نیست.
ان رساله مقدمه هندسه نااقلیدسی جدیدی بود. وی ریاضیات را از قیذ نتها آزاد ساخت و بنیاد هندسه را نیز بر بی نهایت کوچکها گذاشت و هندسه دیفرانسیل را طرح کرد. آزاد ساخت وبنیاد هندسه را نیز بر بی نهات کوچکها گذاشت
و هندسه دیفرانسیل را طرح کرد. پژوهشهای ریمان را هلم هتز و لی و بل ترامی بلیایی و لباچفسکی هر قدر در کار خود پیش رفتند با ناسازگاری دستگاه رو به رو نشدند انما به طور منجز هم سازگار آن را ثابت نکردند. هندسه ریمانی با هندسه بلیایی و لباچفسکی فرق بارز دغاد، مثلا آنان به رسم بیشتر از یک خط به موازات خط معین از نقطه معین قائل بودند، اما ریمان وازی را انکاررد. با این که آنها مجموع زاویه های مثلث را کوچکتر از دو قائمه گرفتند و ریمان بزرگتر از آن.
هندسه نااقلیدسی لیایی و لباچفسکی را هندسه هذلولوی(یپربولیک) و هندسه ریمان را هندسه بیضی (الیپتیک) نامیده اند.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |
|
کاربران در حال دیدن موضوع: 1 نفر (0 عضو و 1 مهمان)
|
|
|
 مجوز های ارسال و ویرایش
مجوز های ارسال و ویرایش
|
شما نمیتوانید موضوع جدیدی ارسال کنید
شما امکان ارسال پاسخ را ندارید
شما نمیتوانید فایل پیوست در پست خود ضمیمه کنید
شما نمیتوانید پست های خود را ویرایش کنید
اچ تی ام ال غیر فعال می باشد
|
|
|
اکنون ساعت 05:11 AM برپایه ساعت جهانی (GMT - گرینویچ) +3.5 می باشد.
|










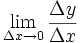

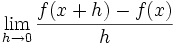
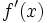
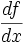
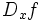
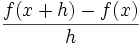
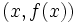
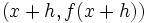
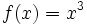
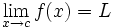
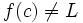
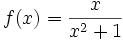
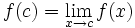
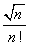
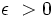

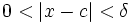

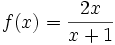
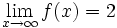
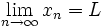
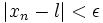
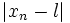
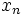
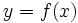

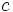
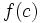
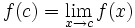
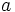
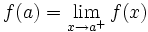
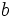
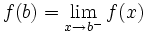
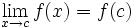
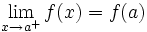
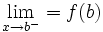
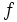

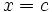
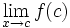

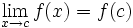
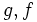
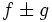
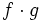
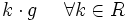

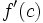
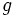
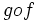
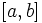
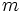
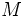
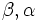
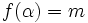
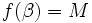
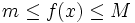
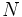
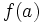
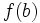
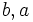

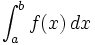
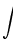
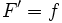
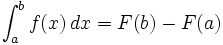

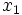
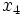
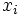
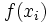
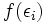
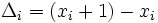
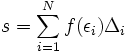

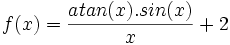

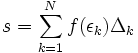
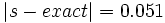
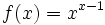
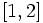
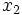
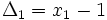
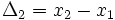
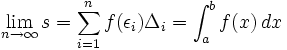
 حالت خطی
حالت خطی

