| فنی و مهندسی در این زیر تالار به بحث و گفتگو در مورد رشته های فنی و مهندسی پرداخته میشود |

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 انتگرالهای چند گانه
انتگرالهای چند گانه
انتگرالهای چند گانه
- انتگرال دو گانه
- انتگرال دو گانه روی نواحی مستطیلی
- قضیه فوبینی (صورت اول):
- قضیه فوبینی (صورت قوی تر):
- دامنه در انتگرال دو گانه
- برخی از انواع دامنههای منظم در انتگرال دو گانه
- تعویض انتگرال ها ی دوگانه
- ویژگیهای انتگرال دوگانه
- انتگرال دوگانه درمختصات قطبی
- تبدیل انتگرال دوگانه در مختصات دکارتی به انتگرال دوگانه در مختصات قطبی
- انتگرال سهگانه
- رابطه بین مختصات دکارتی، استوانهای و کروی
- مباحث مرتبط با عنوان
انتگرال دو گانه
همانطور که تعریف مساحت زیر منحنی انگیزه تعریف انتگرال توابع با یک متغیر است، مفهوم حجم زیر یک سطح نیز ما را به تعریف انتگرال توابع با دو متغیر ، به نام انتگرال دو گانه ، رهنمون می کند. انتگرال دو گانه بسیار شبیه انتگرال میباشد، با این تفاوت که در این نوع انتگرال قلمرو در صفحه دو بعدی واقع شده است.
انتگرال دو گانه روی نواحی مستطیلی
فرض می کنیم بر ناحیه ی مستطیلی زیر تعریف شود:
و فرض می کنیم با شبکه ای از خطوط موازی با محور های و پوشیده شده باشد. مساحت هر کدام از این قطعه های کوچک برابر است با :
این قطعات را شماره گذاری می کنیم و در هر قطعه ای مانند نقطه ی را بر می گزینیم و مجموع زیر را تشکیل می دهیم:
اگر در سراسر پیوسته یاشد، با کوچک کردن خانه های شبکه یعنی میل دادن و به صفر،مجموع مشخص شده در رابطه ی فوق به حدی میل می کند که آن را انتگرال دوگانه ی روی می نامیم.
نماد انتگرال دوگانه عبارت است از :
یا
بنابر این:
قضیه فوبینی (صورت اول):
اگر بر ناحیه مستطیلی پیوسته باشد، داریم:
قضیه فوبینی (صورت قوی تر):
فرض می کنیم روی ناحیه ای چون پیوسته باشد. - اگرتعریف عبارت باشد از : ، با این شرط که و بر پیوسته باشد، آنگاه :
- اگرتعریف عبارت باشد از : ، با این شرط که و بر پیوسته باشد، آنگاه :
دامنه در انتگرال دو گانه
دو دامنه در انتگرال دو گانه وجود دارد: - دامنه منظم: دامنهای است که هر خط موازی محورهای مختصات محیط آن را حداکثر در دو نقطه قطع کند. مانند مربع ، مثلث ، دایره. در این نوع دامنه تعویض حدود انتگرال نسبتا ساده است.
- دامنه غیرمنظم: دامنهای که هر خط موازی محورهای مختصات آن را در بیش از دو نقطه قطع کند مانند سطح بین دو دایره یا دو مربع. در این نوع دامنه ها تعویض حدود باید با احتیاط صورت گیرد.
برخی از انواع دامنههای منظم در انتگرال دو گانه
- : این دامنه به شکل مربع یا مستطیلی است که اضلاع آن موازی محورهای مختصات است.
- دامنههای مثلثی مانند: و در صورت تعویض انتگرال گیری میتوان آن را به صورت نوشت.
- دامنههای دایرهای؛ دامنههای دایرهای در دستگاه دکارتی و قطبی به صورت زیر نوشته میشوند:
دایرهای که مرکز آن در مبدا مختصات و شعاع آن باشد. - دکارتی:
- قطبی:
تعویض انتگرال ها ی دوگانه
مانند مشتقات جزئی، انتگرال نیز دارای ترتیب است. وقتی انتگرال به صورت باشد، یعنی باید ابتدا را ثابت فرض کرده و نسبت به متغیر انتگرال گرفت و در مرحله دوم نسبت به انتگرال بگیریم.
چنانچه حدود به صورت و باشد میتوانیم در صورت لزوم را بر حسب تابعی از نوشته و حدود را از روی شکل دامنه بدست آورده و در انتگرال قرار دهیم یا:
که در این صورت میتوان نوشت:
ویژگیهای انتگرال دوگانه
- اگر ناحیه بسته و محدود اجتماع دو ناحیه بسته و محدود باشد، به طوری که تنها در نقاط مرزی مشترک باشند، آنگاه انتگرال دوگانه تابع در ناحیه برابر است با انتگرال دوگانه تابع در بعلاوه انتگرال دوگانه تابع در .
- اگر و روی ناحیه بسته و محدود پیوسته باشند آنگاه انتگرال دوگانه مجموع این دو تابع برابر است با مجموع انتگرالهای هر کدام از این توابع.
- اگر انتگرال دو گانه روی وجود داشته و عدد حقیقی باشد. آنگاه انتگرال دوگانه برابر است با حاصلضرب در انتگرال دوگانه .
انتگرال دوگانه درمختصات قطبی
گاهی محاسبه یک انتگرال دوگانه در مختصات قطبی آسانتر از محاسبه آن درمختصات دکارتی است.
فرض کنیم ناحیه در مختصات قطبی، بین دو نمودار هموار و محدود شده باشد که در آن باشد در این صورت انتگرال دوگانه را میتوان توسط انتگرال مکرر زیر نشان داد:
تبدیل انتگرال دوگانه در مختصات دکارتی به انتگرال دوگانه در مختصات قطبی
برای تبدیل یک انتگرال مکرر در مختصات دکارتی به یک انتگرال مکرر در مختصات قطبی، به جای ، و (یا ) به ترتیب ، و (یا ) قرار داده و حدود انتگرال گیری را به مختصات قطبی تبدیل میکنیم و در نهایت عملیات انتگرال گیری را بر حسب پارامتر های و انجام می دهیم.
انتگرال سهگانه
انتگرال سهگانه در مورد توابع سه متغیره ی حقیقی تعریف میشود. این تعریف مشابه با تعریف انتگرال دوگانه توابع دو متغیره است. در حالت کلی ، و است.
در دستگاه ها ی مختصات مختلف، انتگرال سه گانه به صورت زیر نوشته میشود: - دستگاه مختصات دکارتی:
- دستگاه مختصات استوانهای: همان طور که محاسبه برخی از انتگرال های دوگانه در مختصات قطبی آسانتر از محاسبه آنها در مختصات دکارتی است، برخی از انتگرال های سهگانه نیز در دستگاه غیر دکارتی سادهتر محاسبه میشوند. یکی از این دستگاههای مختصات، مختصات استوانهای است.
فرض میکنیم مختصات دکارتی نقطه ی P در فضا باشد. اگر مختصات قطبی نقطه ی باشد، آنگاه را مختصات استوانهی مینامیم.
رابطه بین مختصات دکارتی، استوانهای و کروی
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |
|
جای تبلیغات شما اینجا خالیست با ما تماس بگیرید
|
|

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 انتگرال نامعین
انتگرال نامعین
انتگرال نامعین
- انتگرال نامعین
- انتگرال نامعین
- خواص انتگرال
- انتخاب مقدار ثابت انتگرالگیری
- انتگرالگیری به کمک تغییر متغیر
- انتگرالگیری به روش جزء به جزء
- همچنین ببینید
انتگرال نامعین
اگر پاد مشتق باشد ، آنگاه به ازای هر مقدار ثابت یک پاد مشتق است.زیرا اگر آنگاه:
نکته
اگر جوابی برای باشد ، فرمول همه جوابها را به دست میدهد.
انتگرال نامعین
مجموعه همه پاد مشتقهای یک تابع چون را انتگرال نامعین نسبت به مینامند و با نشان میدهند.
هرگاه فرمول همه پادمشتقهای را به دست دهد، آنرا چنین مشخص میکنیم :
تابع را انتگرال ده انتگرال و را ثابت انتگرالگیری مینامیم. همچنین نشان میدهد که متغیر انتگرالگیری است.
خواص انتگرال
- انتگرال مشتق یک تابع مشتقپذیر برابر است با به علاوه یک ثابت دلخواه.
- یک ثابت را میتوان از زیر نماد انتگرالگیری بیرون آورد.(توجه شود که عباراتی را که توابعی از متغیر انتگرالگیری اند ، نمیتوان از زیر نماد انتگرالگیری بیرون آورد.)
- انتگرال مجموع دو تابع برابر مجموع انتگرالهای آنهاست.این مطلب را میتوان به مجموع هر تعداد متناهی از توابع تعمیم داد.
فرمول های انتگرال گیری
در این دستورها یا متغیر مستقل است و یا تابعی مشتقپذیر از متغیر مستقل دیگری است.
اگر آنگاه
انتخاب مقدار ثابت انتگرالگیری
در حل یک معادله دیفرانسیل مانند معمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.بدین منظور نخست جواب عمومی را تعیین میکنیم که همه جوابهای ممکن را به دست میدهد . سپس مقداری از را تعیین میکنیم که جواب خاص مطلوب را به دست دهد.
اگر نقطهای چون از دامنه را در نظر بگیریم و مقدار دلخواه را برگزینیم ، میتوان با قرار دادن و در معادله و حل آن نسبت به جوابی را یافت که از نقطه بگذرد.به این ترتیب داریم یا .
خم خمی است که از میگذرد.
انتگرالگیری به کمک تغییر متغیر
در حل انتگرالها با روش تغییر متغیر ، به جای تابع پیوسته و مشتق پذیر را قرار می دهیم، یعنی :
بعد از حل ، بر اساس تابع معکوس ، به جای نسبت به قرار میدهیم . یعنی:
از فرمول فوق به صورت زیر هم میتوان استفاده کرد:
انتگرالگیری به روش جزء به جزء
دستور موسوم به انتگرالگیری به روش جزء به جزء است که در آن توابعی مشتقپذیر از هستند. اگر انتگرال به صورت حاصلضرب یک تابع لگاریتمی یا یک تابع معکوس مثلثاتی ، در یک چند جمله ای باشد، در این صورت معمولا را تابع لگاریتمی یا تابع معکوس مثلثاتی انتخاب میکنند ولی اگر انتگرال حاصلضرب یک تابع لگاریتمی یا یک تابع نمایی در یک تابع جبری باشد ، معمولا تابع جبری را فرض میکنند.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 جدول انتگرال توابع گنگ
جدول انتگرال توابع گنگ
جدول انتگرال توابع گنگ
توجه داشته باشید که :
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 جدول انتگرال توابع لگاریتمی:
جدول انتگرال توابع لگاریتمی:
جدول انتگرال توابع لگاریتمی:
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 جدول انتگرال توابع نمایی:
جدول انتگرال توابع نمایی:
جدول انتگرال توابع نمایی:
بطوریکه:
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 جدول انتگرال توابع مثلثاتی
جدول انتگرال توابع مثلثاتی
جدول انتگرال توابع مثلثاتی
انتگرال توابع مثلثاتی شامل sin
where cvs{x} is the [Coversine]] function
انتگرال توابع مثلثاتی شامل cos
انتگرال توابع مثلثاتی شامل tan
انتگرال توابع مثلثاتی شامل cot
انتگرال توابع مثلثاتی شامل sec
انتگرال توابع مثلثاتی شامل csc
انتگرال توابع مثلثاتی شامل sin , cos
همچنین:
همچنین:
همچنین:
همچنین:
همچنین:
انتگرال توابع مثلثاتی شامل sin , tan
انتگرال توابع مثلثاتی شامل cos ,tan
انتگرال توابع مثلثاتی شامل sin , cot
انتگرال توابع مثلثاتی شامل cos ,cot
انتگرال توابع مثلثاتی شامل tan , cot
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 جدول انتگرال توابع هیپربولیک
جدول انتگرال توابع هیپربولیک
جدول انتگرال توابع هیپربولیک
همچنین:
همچنین:
همچنین:
همچنین:
همچنین:
همچنین:
همچنین:
همچنین:
همچنین:
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 جدول انتگرال توابع گویا
جدول انتگرال توابع گویا
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-29-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 جدول انتگرال معکوس توابع مثلثاتی
جدول انتگرال معکوس توابع مثلثاتی
جدول انتگرال معکوس توابع مثلثاتی
Arcsin
Arccos
Arctan
arccot
Arcsec
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-31-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 خصوصیات چهارها
خصوصیات چهارها
خصوصیات چهارها
- اهداف چهارها
- خصوصیات شخصی چهارها
- خصوصیات اجتماعی چهارها
- مباحث مرتبط با عنوان
رمز موفقیت در زندگی چهارها، ثابت قدم بودن است. اینان در وجهه مثبت، افرادی صبور – واقعبین – دارای احساس و منطقی متعادل و پیش رونده هستند و اگر از استعداد خود بهره کافی بگیرند، توفیقات خوبی در زندگی به دست خواهند آورد. اما در وجهه منفی، بسیار عجول – زیاد خواه – بدون پشتکار – و اغلب دارای حالات و افکار متغیر هستند .
اهداف چهارها
- ابتدا این که هدف آنها بزرگ یا کوچک است و یا اهداف مادی یا معنوی است، نباید حائز اهمیت باشد. مهم این است که قوای درونی آنان از حالت ایستایی خارج و با تعقیب عمی هدفها پویا شود. پس از این که قوای درونی آنها از حالت ایستایی خارج شد و به همراه آن، افکار و عواطف و احساستشان نظم گرفت، آن وقت میتوانند اهداف بزرگتر را دنبال کنند.
- هدف اصلی چهارها در این جهان، رسیدن به امنیت روانی و ارتقاء روحی است. این افراد جهت رسیدن به این مقصود، ابتدا بایستی در درون به ثبات عاطفی و ذهنی و احساسی برسند،سپس با اشتیاق – تعهد – صبر – هدف خود را دنبال کنند.
- چهارها قبل از هر چیز بایستی اهداف زندگیشسان را مشخص کنند. سپس با این تعهد وا اراده که همه قوای خود را در آن جهت به کار خواهند گرفت، به سوی اهداف خود حرکت کنند.
- هرگونه دستاوری در این جهان، سرچشمهاش قصد و نیتی روشن، و همچنین اراده و کوششی متمرکز بوده و هست. همان طور که برای احداث یک ساختمان ابتدا باید پی آن را مستحکم کرد، قصد و اراده نیز پی و زیربنای دستیابی به اهداف خواهد بود.
خصوصیات شخصی چهارها
- اکثر چهارها تمایلات و حرکتی متناقض دارند. گاه میخواهند پلههایترقی را چند تا یکی طی کنند. گاهی مدتها در یک پله دچار وسواس شده و درجا میزنند. علت اصلی این تناقض این است که آنان قبل از رسیدن به هدف قبلی، به سوی هدفهای بعدی میروند.
- چهارها ابتدا بایستی انرژی زیربنایی را مستحکم کنند. سپس با قدرت و اعتماد به نفس بیشتر، پیگیر اهداف خود باشند. آنان در اغلب موارد تا آستانه موفقیت نزدیک میشوند، اما چون برای رسیدن به آن تعجیل میکنند، گاه ناامید شده و از ادامه راه باز میمانند.
- چهارها اگر بتوانند با مثبت اندیشی، هماهنگی و ثبات لازم را بین افکار و احساسات خود به خود بیاورند، و در ضمن حس مسئولیتپذیری را در خود تقویت نمایند، به توفیقات خوبی در زندگی دست خواهند یافت.
- چهارها اگر به خود نیایند و خود را افکار و احساسات منفی رها کنند، گاه تا حد هستریک پیش خواهند رفت و یا ممکن است در حالتی از گیجی و پریشان حالی و بی تصمیمی گرفتار شوند.
- چهارها در وجهه مثبت و در شرایط مناسب، دارای عقاید و افکار سازنده هستند. آنان مشاوران مدیران – معاونان و همکاران خوبی در امور مختلف از جمله در امر تجارت و معاملات خواهند بود.
خصوصیات اجتماعی چهارها
- چهارها در روابط اجتماعی نیز چنین عمل میکنند به سرعت با دیگران دوست میشوند، اما با اولین تفاهم و مشکل، دوستیشان را به هم میزنند. یا اغلب در حال تغییر شغل هستند. خانه عوض میکنند. رابطهها را تغییر میدهند و ... حال آن که آنان برای رسیدن به موافقیت در زندگی، نیاز به استقامت و ثبات و پایداری دارند.
- چهارها اغلب در زندگی خانوادگی دچار مشکل میشوند. بعضی از این افراد اغلب با یکی از اعضای خانواده در اختلاف هستند. بعضی دیگر از چهارها در کودکی یا نوجوانی، پدر یا مادر خود را از دست میدهند یا به طریقی از سرپرستی و محبت آنان محروم میشوند. یا ممکن است مورد سختگیری و گاه آزار و اذیت والدین یا دیگر اعضاء خانواده قرار بگیرند.
- چهارها اغلب خود والدین خوبی میشوند. ”آن دسته از چهارها که گرفتار محرومیتها و مشکلات بودهاند اغلب توجه بیشتری نسبت به فرزندان خود دارند. همچنین این افراد به دلیل رنج و سختی که در گذشته با آن مواجه بودهاند، آسان نمیتوانند گذشته را فراموش کنند و چنان مسائل را از پهنه ذهن و فکر پاک کنند. این افراد خوب است از تمرینات تمرکزی و ریلاکسیشن بهره بگیرند.
- چهارها قبل از هر چیز در زندگی، نیاز به ثبات و پایداری دارند. آنان بایستی ابتدا هدفهای کوچک را پی بگیرند و با صبر و استقامت به آنها دست یابند، سپس با قدرت و اعتماد به نفس کافی، به سوی هدفهای بزرگتر حرکت کنند.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |
|
کاربران در حال دیدن موضوع: 1 نفر (0 عضو و 1 مهمان)
|
|
|
 مجوز های ارسال و ویرایش
مجوز های ارسال و ویرایش
|
شما نمیتوانید موضوع جدیدی ارسال کنید
شما امکان ارسال پاسخ را ندارید
شما نمیتوانید فایل پیوست در پست خود ضمیمه کنید
شما نمیتوانید پست های خود را ویرایش کنید
اچ تی ام ال غیر فعال می باشد
|
|
|
اکنون ساعت 09:23 PM برپایه ساعت جهانی (GMT - گرینویچ) +3.5 می باشد.
|








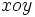


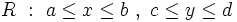

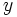
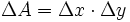
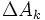
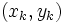
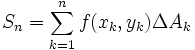
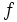
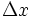
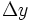
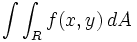
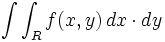
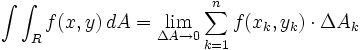
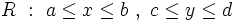
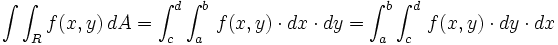
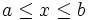
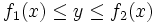
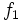
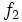
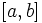
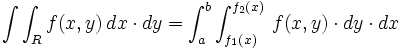

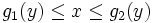
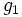
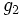
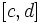
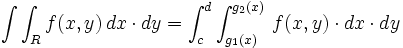
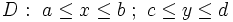
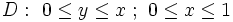
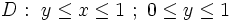
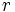
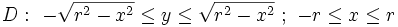
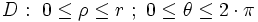
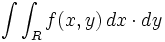
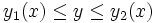

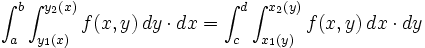
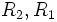
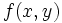
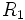
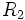

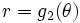
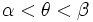
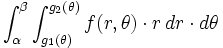
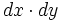
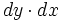
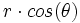
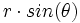
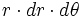
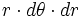

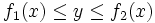
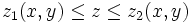
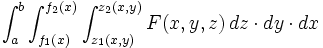
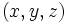
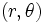
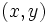
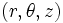
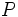
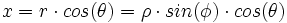
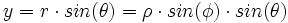
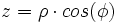
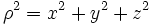

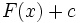
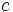
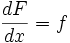
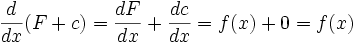

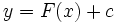
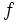
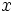
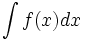
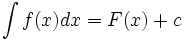
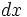
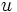
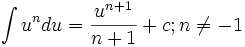
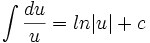
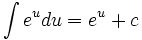
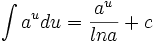

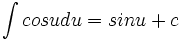
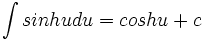
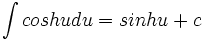
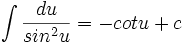
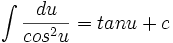
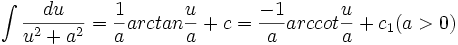
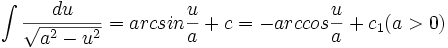
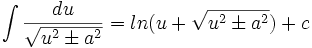
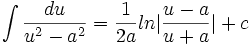
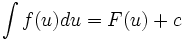

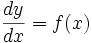
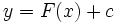
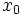
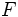
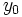
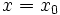
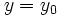
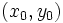
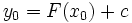
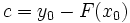
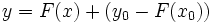
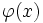

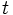
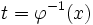
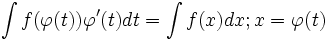
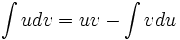
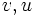
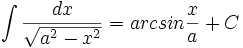
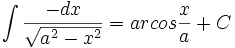
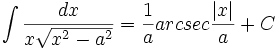
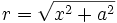
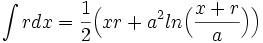
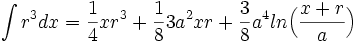
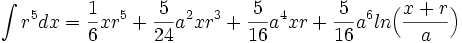
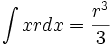
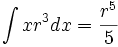
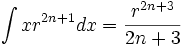

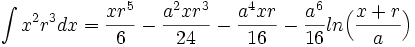

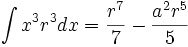
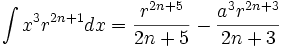
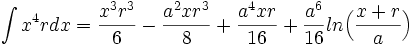
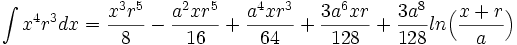

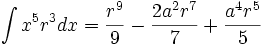
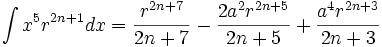
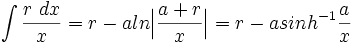
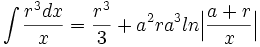
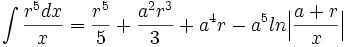
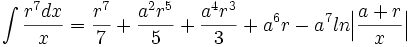
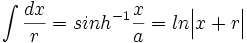
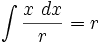
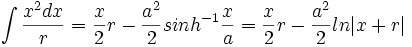
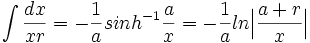
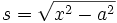
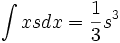
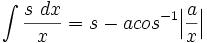
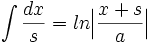
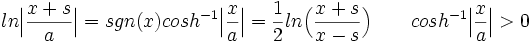
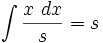
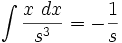
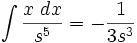
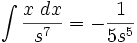
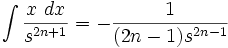
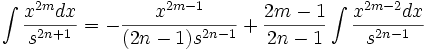
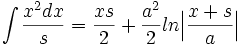
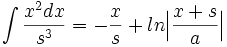
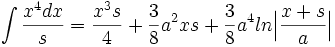
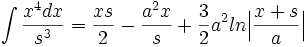
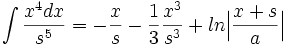
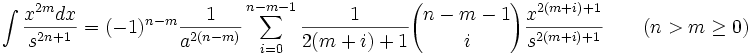

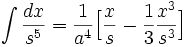
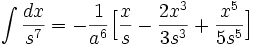
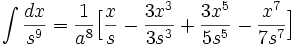
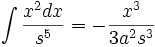
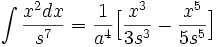
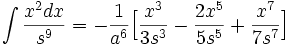

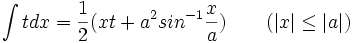
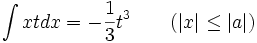
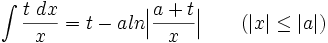
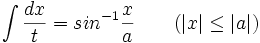
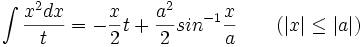

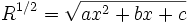
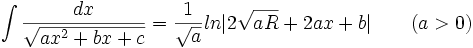
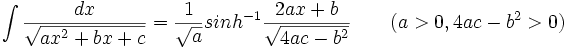
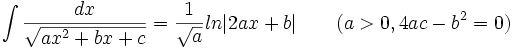
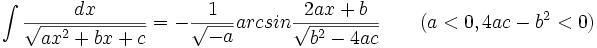
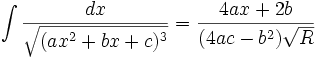
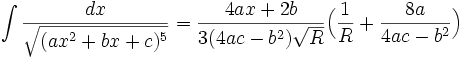

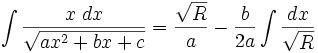
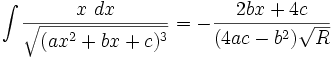
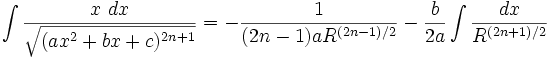
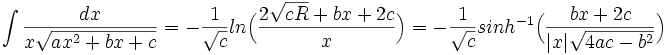
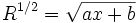
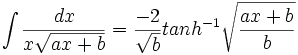
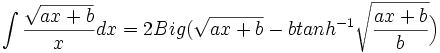
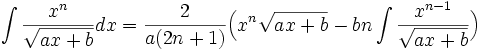
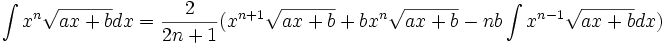
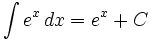
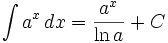
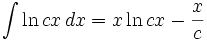
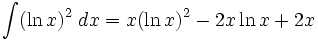
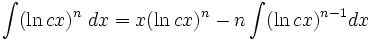
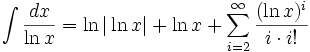
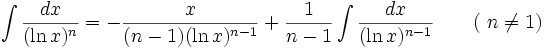
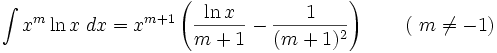
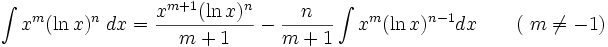
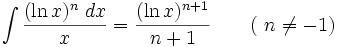
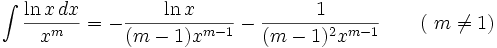
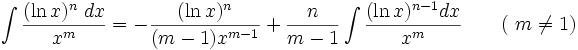
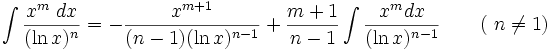
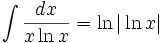

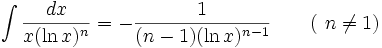
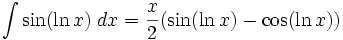
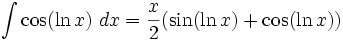

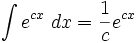
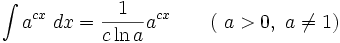
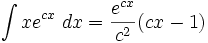
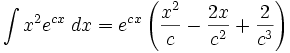
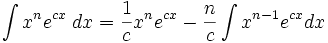
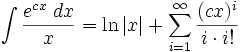
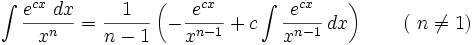
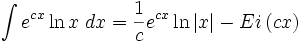
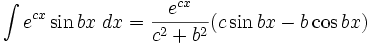
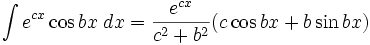
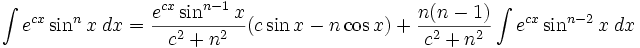
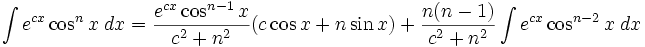
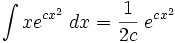
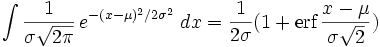
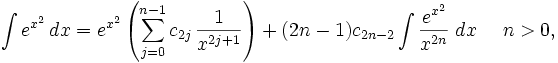
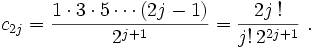
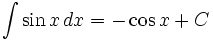
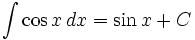
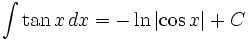
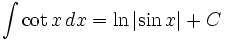
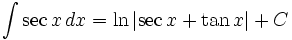
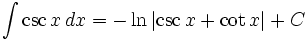
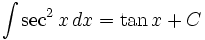
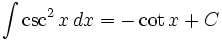
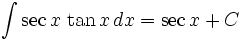
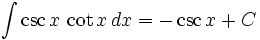
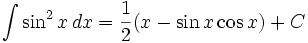
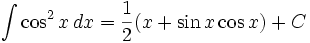
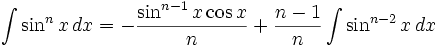
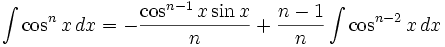
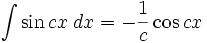
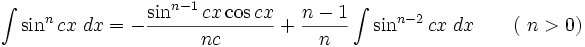
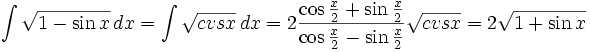
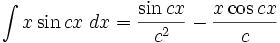
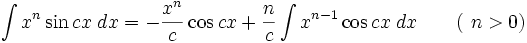
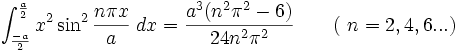
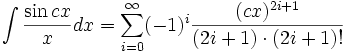
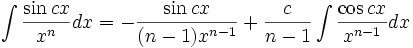
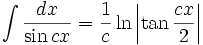
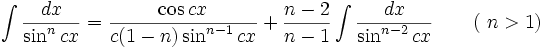
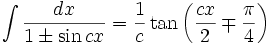
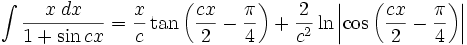

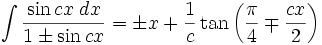
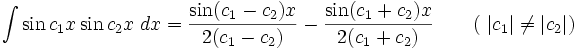
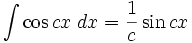
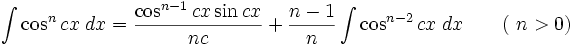
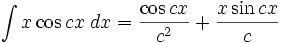
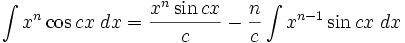
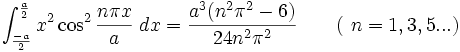
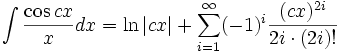
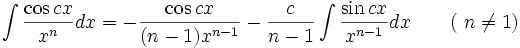
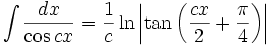
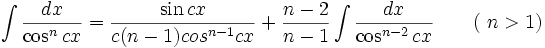
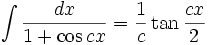
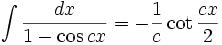
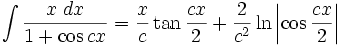
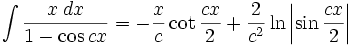
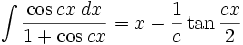
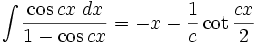
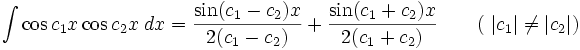
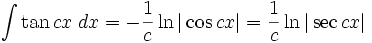
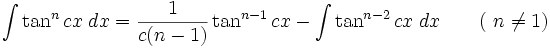
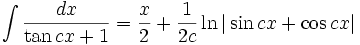
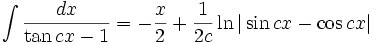
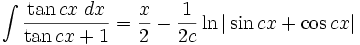
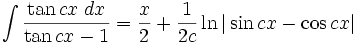
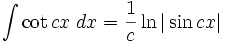
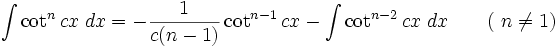
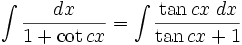
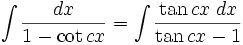
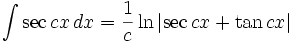
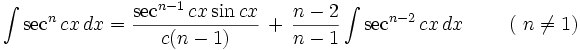
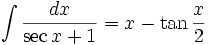
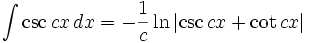
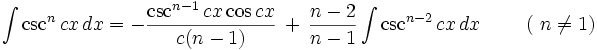
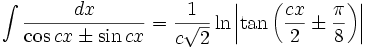
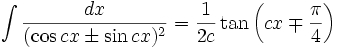
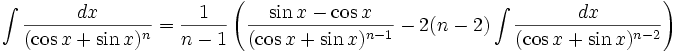
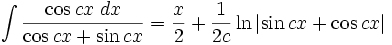
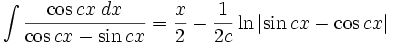
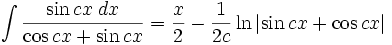
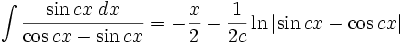
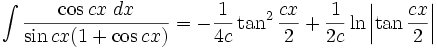
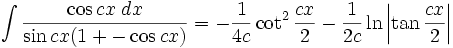
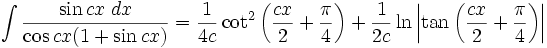
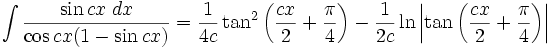
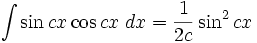
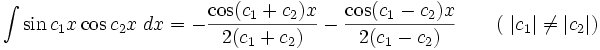
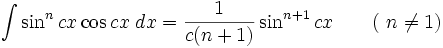
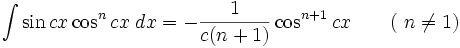
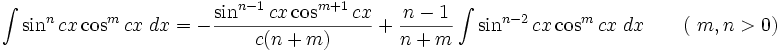
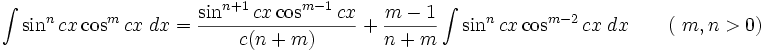
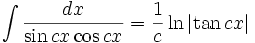
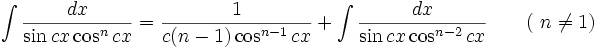
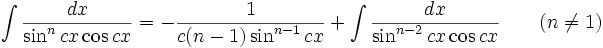
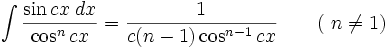
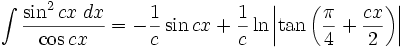
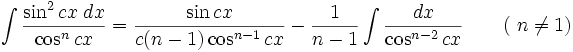
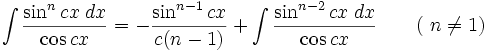
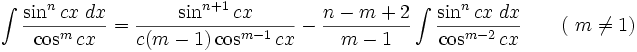
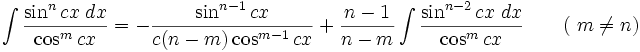
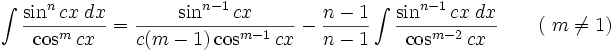
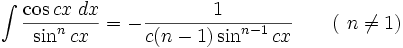
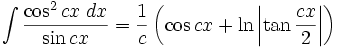
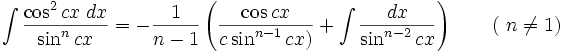
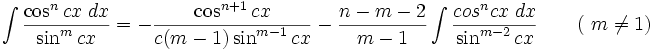
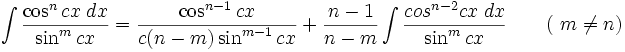
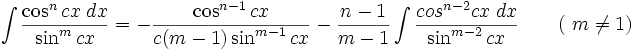
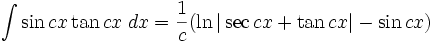
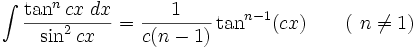
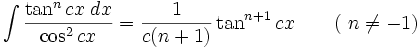
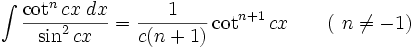
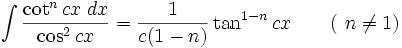

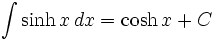
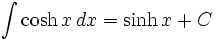
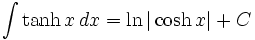
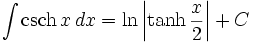
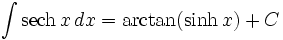
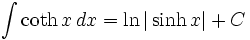
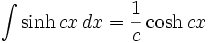
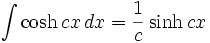
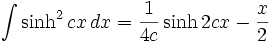
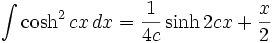
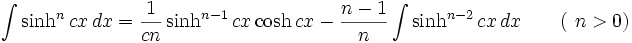
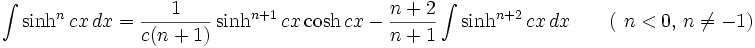
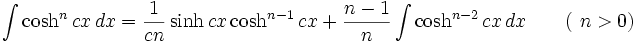
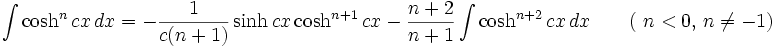
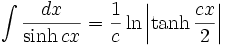
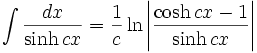
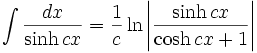
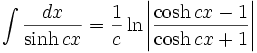
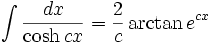
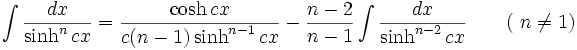
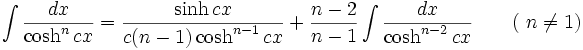
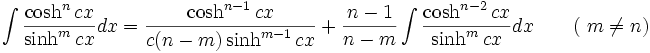
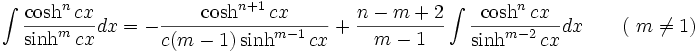
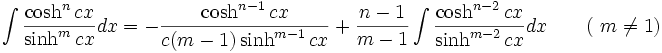

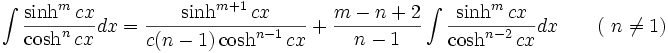
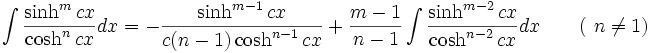
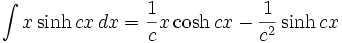
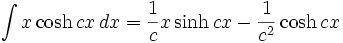
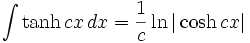
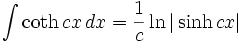
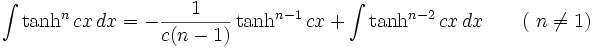
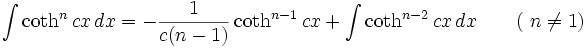
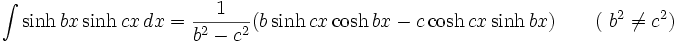
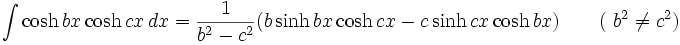
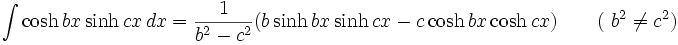
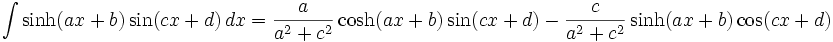
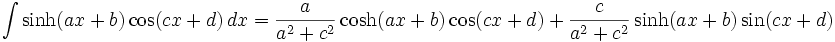
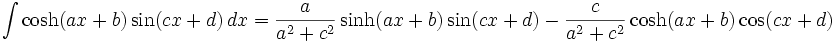

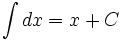
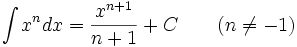
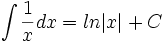
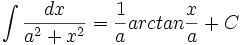
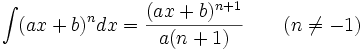
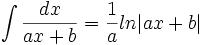
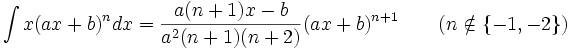
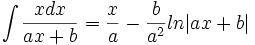
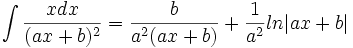
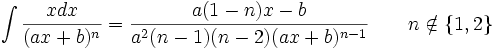
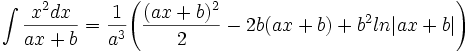
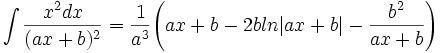
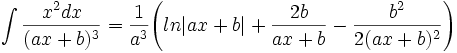

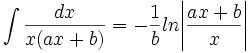
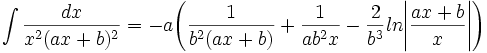
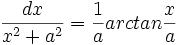
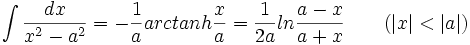
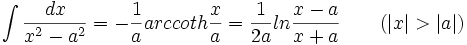
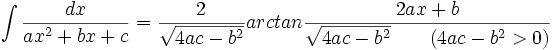
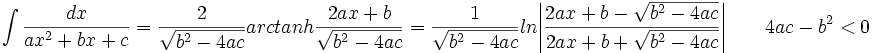
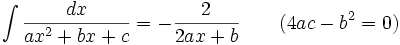
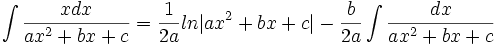
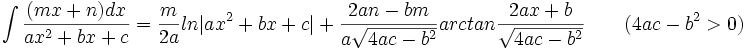
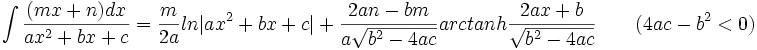
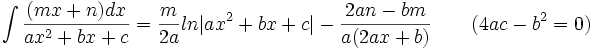
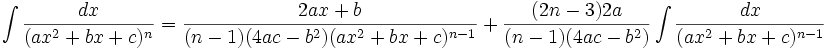
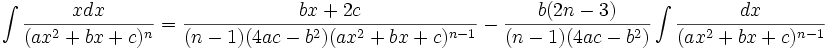
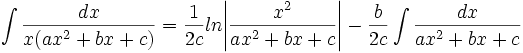
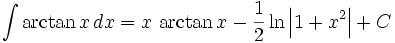
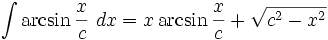
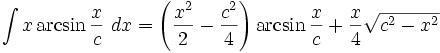
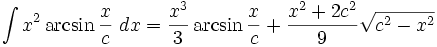
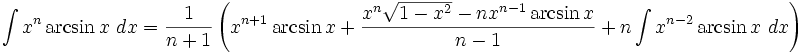
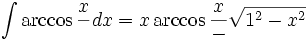
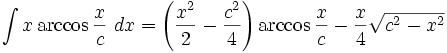
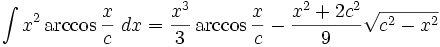
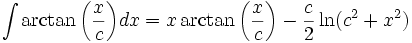
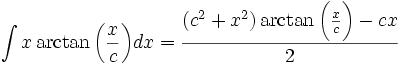

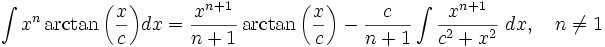

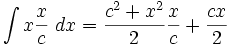
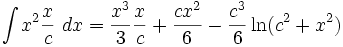
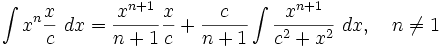
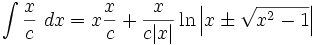
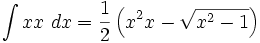
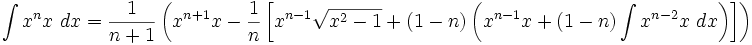
 حالت خطی
حالت خطی

