
|
|
|||||||
| فنی و مهندسی در این زیر تالار به بحث و گفتگو در مورد رشته های فنی و مهندسی پرداخته میشود |
 |
|
|
ابزارهای موضوع | نحوه نمایش |
|
#41
|
||||
|
||||
مدل بازاریابان حرفهای
__________________
زمستان نیز رفت اما بهارانی نمی بینم بر این تکرارِ در تکرار پایانی نمی بینم به دنبال خودم چون گردبادی خسته می گردم ولی از خویش جز گَردی به دامانی نمی بینم چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت! که غیر از مرگ، گردن بند ارزانی نمی بینم زمین از دلبران خالی است یا من چشم ودل سیرم؟ که می گردم ولی زلف پریشانی نمی بینم خدایا عشق درمانی به غیر از مرگ می خواهد که من می میرم از این درد و درمانی نمی بینم استاد فاضل نظری |
| کاربران زیر از رزیتا به خاطر پست مفیدش تشکر کرده اند : | ||
| جای تبلیغات شما اینجا خالیست با ما تماس بگیرید | |
|
|
|
|
#42
|
||||
|
||||
|
مرسی رزیتا خانم
میتوسنتی موضوع رو مهم کنی ...
__________________
مرا سر نهان گر شود زير سنگ -- از آن به كه نامم بر آيد به ننگ به نام نكو گر بميــرم رواست -- مرا نام بايد كه تن مرگ راست |
|
#43
|
||||
|
||||
جوهر و درونمایه ریاضیات
__________________
زمستان نیز رفت اما بهارانی نمی بینم بر این تکرارِ در تکرار پایانی نمی بینم به دنبال خودم چون گردبادی خسته می گردم ولی از خویش جز گَردی به دامانی نمی بینم چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت! که غیر از مرگ، گردن بند ارزانی نمی بینم زمین از دلبران خالی است یا من چشم ودل سیرم؟ که می گردم ولی زلف پریشانی نمی بینم خدایا عشق درمانی به غیر از مرگ می خواهد که من می میرم از این درد و درمانی نمی بینم استاد فاضل نظری |
|
#44
|
||||
|
||||
تاریخ ریاضی
__________________
|
|
#45
|
||||
|
||||
50 فعاليت ساده براي والدين و فرزندان كه به بچه ها كمك ميكند تاابد عاشق رياضيات شوند .هر فعاليت دستورالعمل ساده اي دارد وميگويد كه چگونه درزندگي روزمره خود كاربرد رياضي را پيدا كنيد وچگونه فرزندتان رابراي دانستن بيشتر تشويق كنيد.
__________________
|
|
#46
|
||||
|
||||
 سودوکو
سودوکو
سودوکو تاریخچه:
__________________
|
|
#47
|
||||
|
||||
 معرفي يک دنباله در اعداد طبيعي و بررسي ويژگي هاي آن چکيده
معرفي يک دنباله در اعداد طبيعي و بررسي ويژگي هاي آن چکيده
معرفي يک دنباله در اعداد طبيعي و بررسي ويژگي هاي آن چکيده
__________________
|
|
#48
|
||||
|
||||
احتمال یکی از ابزارهای اساسی علم آمار است که آغاز رسمی آن به قرن هفدهم برمیگردد. در این قرن بازیهایی که در آن شانس ، دخالت بسزایی داشته رایج بوده است. این بازیها همان طور که از اسم آن پیداست کارهایی از قبیل چرخاندن چرخ ، ریختن یک تاس ، پرتاب یک سکه و غیره را دربرمیگیرد. که در آنها برآمد آزمایش ، قطعی نیست. به هر حال واضح است که حتی با وجود قطعی نبودن برآمد هر آزمایش ویژه به یک برآمد قابل پیش بینی در دراز مدت وجود دارد.
__________________
|
|
#49
|
||||
|
||||
 کنج
کنج
کنج
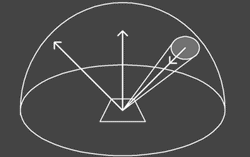 کنج زیر مجموعه ای از فضاست که از اجتماع چند زاویه پدید می آید. چنان که آن زاویه ها راس مشترک دارند و هر یک از آنها در هر ضلع، با یک زاویه دیگر، و تنها با همان زاویه، ضلع مشترک دارد، و هیچ دو زاویه ای در کی صفحه واقع نیستند. راس مشترک زاویه ها، راس کنج؛ هر زاویه را یک زاویه کنج، ضلع مشترک هر دو زاویه مجاور، یال کنج، قسمتی از صفحه هر زاویه را که بین دو ضلع آن محصور است وجه، و فرجه بین هر دو وجه مجاور را یک فرجه کنج می نامند. کنج با تعداد وجه هایش مشخص می شود. ساده ترین کنجها، کنج سه وجهی است. انواع کنج کنج سه قائمه کنج سه وجهی مستقیم کنج کاو کنج کوژ کنج مستقیم کنج قرینه
__________________
|
| کاربران زیر از ROJINAjoON به خاطر پست مفیدش تشکر کرده اند : | ||
|
#50
|
||||
|
||||
 اصل لانه کبوتری!
اصل لانه کبوتری!
با تشکر از روژینای عزیزم برای پستای قشنگش
__________________
|
| کاربران زیر از مهرگان به خاطر پست مفیدش تشکر کرده اند : | ||
 |
| کاربران در حال دیدن موضوع: 1 نفر (0 عضو و 1 مهمان) | |
|
|
اکنون ساعت 06:39 AM برپایه ساعت جهانی (GMT - گرینویچ) +3.5 می باشد.







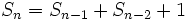
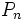



 حالت خطی
حالت خطی

