| فنی و مهندسی در این زیر تالار به بحث و گفتگو در مورد رشته های فنی و مهندسی پرداخته میشود |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 ریاضی و مباحث مرتبط
ریاضی و مباحث مرتبط
ریاضی و مباحث مرتبط
فضای برداری
یک فضای برداری (فضای خطی) متشکل است از:
1.میدان از اسکالرها
2.یک مجموعه از اشیا به نام بردار
3.یک عمل جمع برداری برروی به طوری که به ازای هر متعلق به آنگاه در وجود داشته باشد و
الف.
ب.
ج.
(که در آن منحصر به فرد است.)
د.
4.عمل ضرب موسوم به ضرب اسکالر به طوری که به ازای هر متعلق به و متعلق به عضوی از باشد وداشته باشیم:
الف.
ب.
ج.
د.
در این صورت گوییم یک فضای برداری روی میدان است.
قضیه (1)
فرض کنیم یک فضای برداری بر روی میدان باشد در این صورت:
1.
2.
3.اگر آنگاه یا
4.
5.
(که در آن منحصر به فرد است.)
زیر فضا
فرض کنیم یک فضای برداری بر روی میدان باشد در این صورت اگر همراه با دو عمل جمع برداری روی و ضرب اسکالر تشکیل فضای برداری دهد آنگاه گوییم زیرفضای برداری است.
لم
برای اثبات زیر فضای برداری کافی است بخش های زیر ثابت شود:
1.بسته بودن نسبت به جمع برداری
2.وجود بردار صفر در
3.وجود قرینه هر بردار در
4.بسته بودن نسبت به ضرب اسکالر
قضیه (2)
یک زیر مجموعه غیرتهی از زیرفضاست اگر و فقط:
قضیه (3)
فرض کنیم یک فضای برداری بر روی میدان باشد دراین صورت اشتراک هر دسته دلخواه (نامتناهی) از زیرفضاهای زیرفضاست.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری
ویرایش توسط رزیتا : 10-29-2009 در ساعت 02:17 PM
|
|
جای تبلیغات شما اینجا خالیست با ما تماس بگیرید
|
|

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 جبر برداری
جبر برداری
جبر برداری
مجموع اعمال ریاضی شامل جمع ، ضرب ، مشتق ، انتگرال و... که بر روی بردارها انجام میشود، بر اساس قواعد و اصول خاصی قابل اجراست. مجموعه این قوانین در مبحثی تحت عنوان جبر برداری مورد بحث قرار میگیرند.
اطلاعات اولیه
بحث حرکت در دو یا سه بعد با وارد کردن مفهوم بردار بسیار ساده میشود. یک بردار از نظر هندسی به صورت کمیتی فیزیکی تعریف میشود که بوسیله اندازه و جهت در فضا مشخص میشود. به عنوان مثال میتوان به سرعت و نیرو اشاره کرد که هر دو کمیتی برداری هستند. هر بردار را با یک پیکان که طول و جهت آن نمایشگر اندازه و جهت بردار است، نمایش میدهند. جمع دو یا چند بردار را میتوان بر اساس راحتی کار با استفاده از روشهای متوازی الضلاع یا روش تصاویر که در آن هر بردار را به مولفههایش در امتداد محورهای مختصات تجزیه میکنند، انجام داد.
ضرب بردارها
ضرب بردار در حالت کلی به دو صورت ضرب نقطهای یا عددی و ضرب برداری انجام میشود. در ضرب عددی یا اسکالر یا نقطهای که با نماد A.B نمایش داده میشود، حاصضرب برابر با است با حاصضرب اندازه یک بردار در اندازه تصویر بردار دیگر بر روی آن. طبیعی است که اگر دو بردار بر هم عمود باشند، حاصضرب آنها صفر خواهد بود. اما در ضرب برداری که بصورت A×B نمایش داده میشود، نتیجه حاصضرب ، برداری است که جهت آن با استفاده از قاعده دست راست تعیین میشود و اندازه آن با حاصضرب اندازه دو بردار در سینوس زاویه بین آنها برابراست. ضرب برداری علاوه بر دو حالت فوق میتواند بصورت مختلط نیز باشد. به عنوان مثل اگر C , B , A سه بردار دلخواه باشند در این صورت میتوان ضربهایی به شکل A.B×C یا A×B×C نیز تشکیل داد. اما همواره باید توجه داشته باشیم که نتیجه حاصلضرب اسکالر یا عددی یک عدد است در صورتی که نتیجه حاصلضرب برداری یک بردار است.
قاعده دست راست
قاعده دست راست که در بیشتر مسائل فیزیک که با بردارها سر و کار دارند مطرح است، به این صورت بیان میشود. فرض کنید A و B دو بردار دلخواهی هستند که به صورت برداری در یکدیگر ضرب میشود. برای تعیین جهت بردار حاصضرب کافی است چهار انگشت دست راست را در راستای بردار اول قرار داده و بوسیله چهار انگشت خود این بردار را بطرف بردار دوم بچرخانیم، در این صورت جهت انگشت شست دست راست در راستای بردار منتجه خواهد بود
مشتق گیری برداری
برای مشتق گیری برداری قواعد خاصی وجود دارد که به صورت زیر اشاره میشود.- مشتق جمع دو یا چند بردار با مجموع مشتقات تک تک آنها برابر است.
- مشتق حاصضرب دو بردار (خواه اسکالر خواه برداری) برابر است با مجموع دو جمله ، که جمله اول شامل حاصضرب مشتق بردار اول در خود بردار دوم و جمله دوم برابر با حاصضرب خود بردار اول در مشتق بردار دوم است. بدیهی است که مشتق حاصلضرب چندین بردار نیز به همین صورت تعریف میشود. یعنی به تعداد بردارهایی که در هم ضرب میشوند، جمله وجود دارد و در هر جمله مشتق یک بردار وجود دارد. علاوه بر این مشتقات مراتب بالاتر (مشتق دوم و بیشتر) نیز به همین صورت انجام میشود.
انتگرال گیری برداری
در حالت کلی سه بعدی دو نوع تابع میتوان در نظر گرفت. توابع نقطهای اسکالر و توابع نقطهای برداری. به عنوان مثال تابع انرژی پتانسیل یک تابع نقطهای اسکالر است، در صورتی که شدت میدان الکتریکی یک تابع نقطهای برداری است. همچنین انتگرال گیری نیز میتواند به سه صورت خطی ، سطحی و حجمی صورت گیرد. در حالت اول انتگرال گیری بر روی یک منحنی صورت میگیرد. اما در حالت دوم انتگرال گیری روی یک سطح و سرانجام در حالت چهارم روی یک حجم صورت میگیرد. نکته قابل توجه در اینجا این است که انتگرال گیری با توجه به تقارن موجود و نیز نوع تابع مسئله در سیستمهای مختصاتی مختلف انجام داد. به عنوان مثال اگر مسئله مورد نظر ما دارای تقارن کروی باشد بهتر است کلیه انتگرالهایی که در مسئله مورد نیاز است در سیستم مختصات کروی انجام دهیم.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری
ویرایش توسط رزیتا : 10-29-2009 در ساعت 02:22 PM
|

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 ریاضیات
ریاضیات
ریاضیات
ریاضیات عموما مطالعه الگوی ساختار، تحول و فضا تعریف شده است؛ بصورت غیر رسمی تر، ممکن است بگویند مطالعه "اعداد و اشکال" است. در منظر صاحبان فکر، تحقیق بدیهیات ساختارهای مجرد تعریف شده، با استفاده از منطق و نماد سازی ریاضی میباشد؛ نظرات دیگر در فلسفه ریاضیات بیان شده است.
ساختارهای بخصوصی که در ریاضیات مورد تحقیق و بررسی قرار میگیرند اغلب در علوم طبیعی منشاء دارند، و بسیار عمومی در فیزیک، ولی ریاضیات ساختارهای دلایلی را نیز بررسی می نماید که بصورت خالص در مورد باطن ریاضی است، زیرا ریاضیات می توانند برای مثال، یک عمومیت متحد شده را برای زیر-میدانهای متعدد، یا ابزارهای مفید را برای محاسبات عمومی، فراهم نماید. در نهایت، ریاضیدانان بسیاری در مورد مطالبی که مطالعه می نمایند که منحصرا دلایل علمی محض داشته، ریاضیات را بصورت هنری برای پروراندن علم، صرف نظر از تجربی یا کاربردی، می نگرند.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری
ویرایش توسط رزیتا : 10-28-2009 در ساعت 08:03 PM
|

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 بردار
بردار
بردار
کلمه بردار به معنای حمل کننده میباشد و از یک کلمه لاتین به همین معنا گرفته شده است.یک بردار به عنوان یک عنصر از فضای برداری تعریف میشودو در فضای nبعدی دارای n مولفه است.پس بدیهی است که یک بردار در صفحه دارای دو مولفه میباشدو یا در فضای سه بعدی سه مولفه را اختیار میکند.بردارها در علوم مختلف مانند فیزیک کاربردهای فراوانی دارند و بدون آنها نمیتوان بسیاری از مولفه های فیزیکی مانند سرعت ، شتاب و... را تفسیر و تعریف نمود.
خصوصیات بردارها
بردارها را میتوان با یکدیگر جمع (جمع بردارها) و یا ضرب (ضرب بردارها) کرد.البته ضرب دو بردار با ضرب یک اسکالردر آن فرق میکند.ضرب بردارها سه نوع است که عبارتنداز ضرب داخلی ، ضرب خارجی و ضرب مستقیم تانسوری که حاصل همه این ضربها لزوما یک بردار نیست.
هر بردار دارای دو مولفه است که این دو مولفه عبارتند از طول بردار و جهت بردار.همچنین هر بردار دارای یک ابتدا و یک انتها نیز هست. برداری که دارای طول واحد باشدبردارواحد مینامند و برداری که طول آن صفر است را بردارصفر مینامند.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 ضرب داخلی
ضرب داخلی
ضرب داخلی
در ریاضیات فضای ضرب داخلی یک فضای برداری است. ضرب داخلی یا ضرب اسکالر به ما این امکان را میدهد که مفاهیم هندسی از قبیل زاویه و طول یک بردار را تعریف نماییم.با وجود آنکه در این نوع ضرب دو بردار در هم ضرب میشوند ولی حاصلضرب این دو بردار یک عدد اسکالر است.ضرب داخلی در ریاضیات،مهندسی،وفیزیک کاربردمای فراوانی دارد
تعریف
ضرب داخلی دو بردار uوvرا با نشان میدهند. ضرب داخلی در یک فضای برداری حقیقی از چهار ویژگی مهم تبعیت میکند.فرض کنید u،vوهمچنین w سه بردار ویک اسکالر باشدآنگاه:
1.
2.
3.
4. و برابر صفر است هرگاه v=0 باشد.
تعاریف زیر را برای ضرب داخلی ذکر میکنیم:
1. در حوزه اعداد حقیقی به صورت زیر بدست میآید:
2.در فضای n-بعدی حاصلضرب داخلی از رابطه زیر بدست میآید:
به عنوان مثال در فضای دو بعدی میتوان ضرب داخلی دو بردار را از رابطه زیر محاسبه کرد:
نرم در فضای ضرب داخلی
در فضای ضرب داخلی نرم یک بردار به صورت زیر تعریف میشود:
در واقع بوسیله نرم یک بردار میتوان طول آن بردار رابدست آورد.
نامساوی کوشی-شوارتز
البته دقت کنید که دو برداری که در این نامساوی صدق میکنند باید وابسته خطی باشند.
محاسبه زاویه بین دو بردار
پس از مطالعه این مطالب شاید از خود بپرسید که این روابط دارای چه فوایدی هستند و چه لزومی دارد که این روابط را بدانیم؟
فرض کنید دو بردارداریم که مختصات آنها معلوم است،حال میخواهیم زاویه بین این دو بردار را بدست آوریم برای این کار از فرمول زیر استفاده میکنیم:
باید توجه کرداین فرمول زاویه بین دو بردار را در فضای دو بعدی محاسبه میکند.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
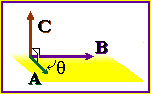
 ضرب خارجی
ضرب خارجی
ضرب خارجی
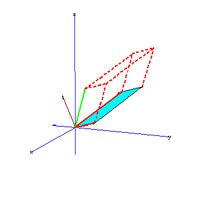
ضرب خارجی که به آن ضرب برداری نیز گفته میشود،یک عمل دوتایی در یک فضای سه بعدی است که بر روی دو بردار اعمال میشود.حاصل این عمل برداری است که بر دو بردار مذکور عمود است.جهت این بردار از طریق قانون دست راست بدست می آید.
تعریف
دو بردار AوB را در نظر میگیریم و زاویه بین این دو بردار را فرض میکنیم در این صورت ضرب خارجی این دو بردار به صورت زیر تعریف میشود:
فرض کنیم دو بردار مذکور بر حسب بردارهای واحد i و j و k و به صورت زیر تعریف شده باشند:
در این صورت ضرب خارجی دو بردار ( بدون نیاز به داشتن زاویه بین آنها) به صورت زیر تعریف میشود:
خصوصیات
خصوصیات هندسی
حجم متوازی السطوحی که روی سه بردار
ساخته شده است از ضرب سه گانه این
سه بردار حاصل میشود.
اندازه ضرب خارجی برابر مساحت یک متوازی الاضلاعی است که بر روی دو ضلع a و b ساخته شده است. یعنی داریم:
همچنین حجم یک متوازی السطوح که بوسیله بردارهای a و b و c ایجاد شده است برابر ضرب سه گانه زیر میباشد:
ویژگیهای جبری
- ضرب خارجی دو بردار خاصیت جابجایی ندارد:
- ضرب خارجی دو بردار خاصیت توزیع پذیری نسبت به عمل جمع دارد:
- ضرب یک عدد اسکالردارای خصوصیت زیر خواهد بود :
- این ضرب شرکت پذیر نیست. ولی در اتحاد ژاکوبی صدق میکند:
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 معادله
معادله
معادله
در ریاضیات، یک معادله از یک یا چندین متغیر تشکیل شده است که میتواند یک یا چندین جواب داشته باشد.در یک معادله دو عبارت در دو سوی یک = قرار دارند.و مقادیری که به ازای آنها دو عبارت موجود،مقداری مساوی دارند را جواب معادله گویند. به عنوان مثال عبارت زیر یک معادله با یک جواب است.
ولی عبارت زیر معادله ای با دو جواب میباشد.
تاریخچه
معادلات همراه با اعداد، از اولین دستاوردهای ریاضی بشرند. آنها در قدیمی ترین اسناد ریاضی، مکتوب، فی المثل، در متون میخی بابلیهای باستان، که به هزاره قبل از میلاد بر می گردند، و پاپیروسهای مصری باستان، که به امپراطوری میانه در حدود 1800 ق.م. بازگشت دارند، آمده اند.
بنا به ساختار جامعه بابلی مسائل مربوط به تقسیم ارث از اهمیت بسیاری برخوردار بودند. اولین پسر همواره بیشترین سهم را دریافت می کرد، دومی بیشتر از سومی، و به همین ترتیب.
در حالی که مسائل مطرح در بابل ،مجهول نسبتاً واضح توصیف شده است، در پاپیروس های مصری با علامت "h" نمایش داده شده است، که توده یا گردایه را نشان می دهد. چنین محاسباتی نسبتاً زیاد رخ می دهند و متناظر با معادلات خطی ما هستند. مقایسه ای بین متنی مصری از پاپیروس مسکو و نماد نویسی جدید این نکته را روشن می سازند.
پیش از این که زبان نمادین جبری مطرح شود، معادلات را بالاجبار با کلمات می نوشتند حتی فرانسواویت که معمولاً به ویتا موسوم است که شایستگی های بسیاری در زمینه جبر دارد از کلمه لاتین برای برابر بودن استفاده می کرد
علامت برابری = که امروزه متداول است توسط روبرت رکورد پزشک دربار سلطنتی مطرح شد، اما زمان قابل ملاحظه ای طول کشید تا این علامت مقبولیت عام یافت.
the whetstone of witte
وی این طرح را در کتاب درسی جبری که به صورت گفتگو نوشته شده بود و عنوانش "the whetstone of witte" بود مطرح و انگیزه انتخاب ان را با گفتن مطالب زیر بیان کرد «در این مورد همان گونه که قالباً در عمل انجام می دهم یک جفت خط توامان می گذارند این چنین = = =, زیرا هیچ دو شیی نمی توانند برابر محض باشند.
با نوشته شدن کتاب جبر و مقابله توسط خوارزمی در سده های سوم و چهارم هجری ،جبر وارد ریاضیات شد، و به حل معادله ها پرداخته شد.خود واژه جبر به معنای جبران کردن و مقابله به معنای روبه رو قرار دادن دو سوی برابری است.
مجموعه جواب
کار با مجموعه معینی از اعداد، موسوم به حوزه اصلی و مجموعه مشخصی از متغیرها که عناصری از حوزه اصلی با زیر مجموعه ای، موسوم به حوزه تغییرپذیری را می توان به جای آنها قرارداد، آغاز می شود.
در مشخص کردن حوزه اصلی و حوزه تغییر پذیری،N به جای مجموعه اعداد طبیعی، Z به جای مجموعه اعداد صحیح،Q به جای مجموعه اعداد گویا،R به جای مجموعه اعداد حقیقی و C به جای اعداد مختلط قرار می گیرد.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 معادله درجه دوم
معادله درجه دوم
معادله درجه دوم
تعریف
دایره ، سهمی ، بیضی و هذلولی هستند که معادلهشان حالتهای خاصی از معادله درجه دوم زیر است:
بطور مثال دایره:
از معادله درجه دوم فوق بدست آورد. در واقع خط راست هم حالت خاصی از معادله درجه دوم است هرگاه ولی این شرایط معادله درجه دوم را به یک معادله خطی بجای معادله درجه دوم بدل میکنند جملات جملات درجه دوم میباشند و در حال حاضر رابطه ذکر شده در تعریف را وقتی که لااقل یکی از این جملات درجه وجود داشته باشند بررسی خواهیم کرد.
تاریخچه
معادلات درجه دوم و اشکال آنها موارد مورد بحث در هندسه تحلیلی سه بعدی هستند. هندسه تحلیلی سه بعدی را ریاضیدانان قرن هفدهم میلادی از قبیل فرما ، دکارت و لاهید ابداع کردند. ولی دستگاه مختصاتی را که ما امروز به کار میبریم ، یوهان برنولی در فاصلهای به لایب نیتس در 1715 صورتبندی کرد. در قرن هجدهم ، آلکسی کلرو (1713-1765) و لئونهارت اویلر (1707-1783) برجسته ترین ریاضیدانانی بودند که هندسه سهبعدی را گسترش دادند.
بخصوص کلرو معلوم ساخت که یک رویه را میتوان با معادلهای بر حسب سه مختصش نشان داد و برای توصیف خمی در فضا ، دو تا از این گونه معادلهها لازم است. او ایدههایش را در کتاب "تحقیق درباره خمهای با خمیدگی مضاعف" در 1731 مطرح کرد وی در این کتاب معادلات چندین رویه درجه دوم از قبیل کره – استوانه – هذلولیوار و بیضیوار را آورد. توجه او در نهایت معطوف به شکل زمین بود که فکر می کرد نوعی بیضیوار باشد. گاسپار موثر هندسهدان پیشرو قرن هجدهم زیرا مطالب زیادی درباره هندسه تحلیلی سه بعدی نوشت.
ساختمان
جمله مخلوط را میتوان با دوران محورها حذف نمود بی آنکه از کلیت مطلب کاسته شود، بنابراین با تبدیل معادله ذکر شده در بخش تعریف به معادله زیر خواهیم داشت:
در این صورت معادله فوق:
- یک خط راست است هرگاه یا یکی از آنها صفر نباشد.
- یک دایره است هرگاه ، در حالات خاص ممکن است که به یک نقطه تبدیل شود و یا هیچ مکان حقیقی بوجود نیاورد.
- یک سهمی است هرگاه نسبت به یکی از متغیرها خطی و نسبت به دیگری از درجه دوم باشد.
- یک بیضی است و هرگاه هر دو مثبت و یا هر دو منفی باشند در حالت خاص ممکن است که بیضی تبدیل به یک نقطه شود و یا هیچ مکان حقیقی بوجود نیارود.
- یک هذلولی است هرگاه غیر از صفر و مختلفالعلامات باشند. در حالات خاص ، مثلا ممکن است که مکان به دو خط متقاطع تبدیل شوند.
برای شناختن منحنی ای که معادلهاش داده شده است:
- محورها را (در صورت لزوم) دوران دهید تا درجه ناحیه مخلوط حذف شود.
- محورها را (در صورت لزوم) انتقال دهید تا معادله به شکلی در آید که قابل تشخیص باشد.
گاهی اوقات مفید است که محکی که مشخص میکند که آیا یک معادله درجه دوم سهمی یا بیضی یا هذلولی است مستقیما در مورد معادله بکار برده شود بیآنکه لازم باشد که آن را بوسیله دوران محورها بصورتی فاقد جمله در آوریم.
با توجه به مطالب بالا اگر محورها را به اندازه زاویهای چون که از رابطه بدست میآید دوران دهیم معادله را به شکل معادل زیر تبدیل میکند:
که در آن ضرایب جدید هستند که به ضرایب قدیم مربوطاند. هر گاه α از رابطه گفته شده انتخاب کنیم در اینصورت حال اگر معادله منحنی مطابق با ضرایب جدیدی اما فاقد جمله باشد آن منحنی:
- سهمی است هرگاه یا (اما هر دو) صفر باشد و هر دو در معادله وجود داشته باشند.
- بیضی است (یا در حالات استثنایی ، یک نقطه ، یا تهی است) هرگاه همعلامت باشند.
- هذلولی است (یا در حالات استثنایی یک جفت خط متقاطع است) هرگاه همعلامت نباشند.
ولی میتوان دید که ، برای هر دوران دلخواهی از محورها رابطه زیر بین A ، B ، C و برقرار است:
یعنی مقدار تحت هر دورانی از محورها بدون تغییر باقی میماند. اما وقتی که دوران خاصی را که را صفر کند انجام دهیم طرف راست معادله فوق به شکل ساده تبدیل میگردد. حالا میتوانیم محک لازم را بر حسب مبین معادله یعنی:
بیان کنیم. میتوان گفت که منحنی:
- سهمی (یا در حالات استثنایی یک جفت متوازی ، یا یک خط یا یک مکان تهی) است هرگاه:
- بیضی است (یا در حالات خاص یک نقطه ، یا تهی) هرگاه:
- هذلولی است ( یا در حالات خاص یک جفت خط متقاطع است) هرگاه:
- باید توجه کرد که اگر در معادله اصلی هیچ جمله درجه اولی وجود نداشته باشد، در معادله جدید هم وجود نخواهد داشت. این مطلب از این حقیقت ناشی میشود که دوران محورها درجه هر جمله از معادله را حفظ میکند.
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 معادله درجه سوم
معادله درجه سوم
معادله درجه سوم
در ریاضیات، معادله درجه 3 یک چند جملهای است که بیشترین درجه مجهول آن 3 باشد. به عنوان مثال معادله یک معادله درجه 3 میباشد، فرم کلی معادلات درجه سوم به صورت نوشته میشود. که بطور معمول ضرایب معادلهای را حقیقی هستند. همچنین، همواره منفی بر اینست که در چنین معادلهای باشد. حل معادله درجه سوم متوجه پیدا کردن ریشههای معادله میباشد.
تاریخچه
معادلات درجه سوم برای اولین بار توسط ریاضیدانان هندسی در حدود 400 سال قبل از میلاد مورد توجه قرار گرفت. در بین ریاضیدانان پارسی، عمر خیام (1123-1048) راه حلی را برای حل معادله درجه سوم ابداع کرد. او در این روش با استفاده از هندسه نشان داد که چگونه با استفاده از روش هندسی میتوان به جواب عددی معادله رسید با استفاده از جدول مثلثاتی. همچنین در حول و حوش قرن 16، یک ریاضیدان ایتالیایی به نام scipione، روشی را برای حل کلاسی از معادلات درجه سوم که به صورت میباشند را ادامه داد. او همچنین نشان داد که تمامی معادلات درجه سوم را میتوان به صورت گفته شده کاهش داد.
ریشههای معادله
هر معادله درجه سوم حقیقی حداقل یک جواب حقیقی دارد. این استدلال نتیجه مستقیم قضیه مقدار میانگین است.
برای معادله درجه سوم یک معادله مشخصهای به صورت زیر بیان میشود که امکان وجود ریشهها را بیان میکند. بنابراین با فرض
موارد زیر نتجه میشود:
- : آنگاه معادله حتما 3 ریشه مجزا خواهد داشت.
- : آنگاه معادله حتما یک ریشه حقیقی و. یک جفت ریشه مختلط خواهد داشت.
- : آنگاه معادله حداقل دو ریشه دارد.
برای تصمیم گیری در مورد اینکه معادله چند ریشه متمایز دارد را به صورت زیر تشکیل میدهیم:
حال دو حالت در نظر میگیریم:
اگر ، آنگاه هر 3 ریشه تکراری است.
در غیر اینصورت معادله 2 ریشه تکراری و یک ریشه مجزا خواهد داشت.
روش کاردانو برای پیدا کردن ریشههای معادله درجه سوم
در ابتدا معادله داده شده را به فرم کلاسیک تبدیل میکنیم، همین معادله داده شده را به ضریب تقسیم میکنیم.
حال با تغییر متغیر: معادله را به فرم زیر تبدیل میکنیم.
بطوری که و معادله به دست آمده را معادله تقلیل یافته مینامیم.
حال فرض میکنیم که بتوانیم اعداد u و v را طوری پیدا کنیم که:
حل جواب معادله داده شده با فرض t=v-u به دست میآید این مطلب بطور مستقیم با تعقیب متغیر t در (2) قابل بررسی میباشد. به عنوان یک نتیجه از اتحاد معادله درجه سوم معادله
(3) قابل حل است. با حل معادله درجه دوم برای v که به دست میآید
با قرار دادن این مقادیر در 3 خواهیم داشت
که از حل این معادله که یک معادله درجه 2 از میباشد خواهیم داشت
حال چون و پس
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |

10-28-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
 معادلات دیفرانسیل
معادلات دیفرانسیل
معادلات دیفرانسیل
مقدمه
معادله دیفرانسیل معادلهای است که شامل یک یا چند مشتق یا دیفرانسیل باشد. معادلات دیفرانسیل بر اساس ویژگیهای زیر رده بندی میشوند:
نوع (عادی یا جزئی)
- معادله شامل متغیر مستقل x ، تابع (y = f(x و مشتقات f را یک معادله دیفرانسیل عادی مینامیم.
- معادله ای متشکل از یک تابع مجهول با بیش از یک متغیر مستقل همراه با مشتقات جزئی آن معادله دیفرانسیل جزئی می نامیم.
مرتبه
که عباترت است از مرتبه مشتقی که بالاترین مرتبه را در معادله دارد.
درجه
نمای بالاترین توان مشتقی که بالاترین مرتبه را در معادله دارد، پس از حذف مخرج کسرها و رادیکالهای مربوط به متغیر وابسته و مشتقاتش. معمولا یک معادله دیفرانسیل مرتبه n جوابی شامل n ثابت دلخواه دارد، این جواب را جواب عمومی مینامند.
ساختار
معادلات دیفرانسیل ساختارهای متفاوتی هستند و هر ساختار ویژگیهای متفاوتی دارد:
- معادلات مرتبه اول از درجه اول
- با متغیرهای جدایی پذیر
- همگن
- خطی (برنولی)
- با دیفرانسیلهای کامل
- معادلات مرتبه دوم
- معادلات خطی با ضرایب ثابت: الف) همگن ب) ناهمگن.
- تکنیکهای تقریب زدن: الف) سریهای توانی ب) روشهای عددی.
صور مختلف معادلات دیفرانسیل
معادله دیفرانسیل مرتبه اول از درجه اول را همواره میتوان به صورت زیر در آورد که در آن M و N معرف توابعی از x و y هستند.
Mdx + Ndy = 0
در معادله فوق هرگاه M فقط تابعی از x و N فقط تابعی از y باشد. به صورت معادله جدایی پذیر مرتبه اول است. در این صورت با انتگرال گیری از هر جمله جواب بدست میآید. یعنی:
M(x) dx+ ∫N(y) dy = C∫
معادله دیفرانسیل همگن
گاه معادله دیفرانسیلی را که متغیرهایش جدایی پذیر نیستند با تعویض متغیر میتوان به معادلهای تبدیل کرد که متغیرهایش جدایی پذیر باشند، چنین معادلهای را همگن مینامند. معادله دیفرانسیل خطی مرتبه اول را همیشه میتوان به صورت متعارف زیر در آورد که در آن P و Q توابعی از x هستند.
dy/dx + py = Q
معادله را که بتوان آن را به صورت:
M (x,y) dx + N(x,y) dy = 0
نوشت و دارای ویژگی زیر باشد کامل نامیده میشود. زیرا طرف چپ آن یک دیفرانسیل کامل است.
M/∂y = ∂N/∂x∂
معادلات دیفرانسیل مرتبه دوم
یک معادله دیفرانسیل مرتبه دوم در حالت کلی به صورت زیر است:
F (x,y,dy/dx,d2y/dx2) = 0
این گونه معادلات را معمولا با یک متغیر مناسب مثل dy/dx = p به معادلات دیفرانسیل نوع اول تبدیل کرد و با جاگذاری در معادله مربوط به روش معادلات دیفرانسیل مرتبه اول حل کرد.
معادلات دیفرانسیل خطی
معادله دیفرانسیل
را که در آن توابع ، ، ... ، و بر بازه I پیوسته بوده و (an(x هرگز صفر نباشد یک معادله دیفرانسیل خطی مرتبه n ام مینامیم. که البته اگر در تعریف فوق (F(x مساوی صفر باشد، معادله دیفرانسیل D برای مشتق توابع معرفی میشود، سپس با نوشتن معادله کمکی p(r) = 0 و پیدا کردن صفرهای معادله (p(r جواب معادله همگن را پیدا میکنیم. در صورت ناهمگن بودن علاوه بر عملیات فوق ، جوابهای معادله ناهمگن را با شیوه های خاصی را پیدا کرده به جواب بالا اضافه میکنیم.
حل معادلات دیفرانسیلی خطی مرتبه n ام به توسط سریهای توانی
معادله دیفرانسیل
را در نظر میگیریم که در آن x0 نقطه منفرد معادلات در این صورت با تغییر متغیر زیر به حل معادله میپردازیم:
همین طور با جاگذاری سری مربوط به (F(x و تجریه مناسب و مساوی قرار دادن دو طرف عبارت به حل معادله میپردازیم.
کاربردها
کاربردهای معادلات دیفرانسیل توصیف کننده حرکت سیارات ، که از قانون دوم نیوتن بدست میآیند، هم شامل شتاب و هم شامل سرعت میشوند.
- در مورد حرکت موشکها در نزدیکی سطح زمین و در فضا ، معادلات دیفرانسیل پیچیده ترند.
- مسائل فیزیکی زیادی بعد از فرمول بندی آنها به زبان ریاضی به معادلات دیفرانسیل منجر میشوند.
- در رشته سینتیک شیمیایی ، معادلات دیفرانسیل نقش منحصر به فردی به عهده دارند.
- همینطور در مواردی چون سود مرکب ، واپاشی رادیواکتیو – قانون سرمایش نیوتن و رشد جمعیت کاربرد فراوانی دارد
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |
|
کاربران در حال دیدن موضوع: 1 نفر (0 عضو و 1 مهمان)
|
|
|
 مجوز های ارسال و ویرایش
مجوز های ارسال و ویرایش
|
شما نمیتوانید موضوع جدیدی ارسال کنید
شما امکان ارسال پاسخ را ندارید
شما نمیتوانید فایل پیوست در پست خود ضمیمه کنید
شما نمیتوانید پست های خود را ویرایش کنید
اچ تی ام ال غیر فعال می باشد
|
|
|
اکنون ساعت 04:01 AM برپایه ساعت جهانی (GMT - گرینویچ) +3.5 می باشد.
|








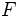
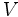
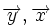
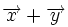
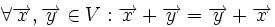
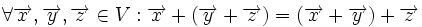
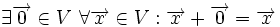
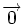
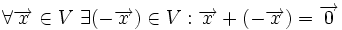

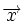
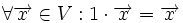
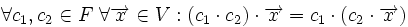
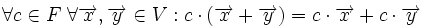
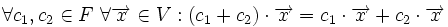
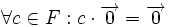
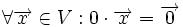
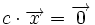
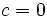
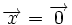
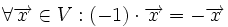
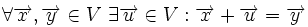
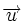
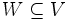
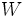
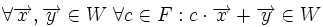


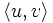
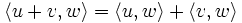
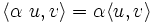
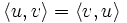
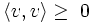
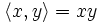
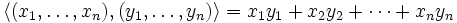
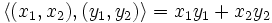
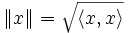
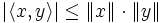
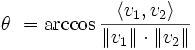
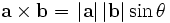
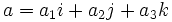
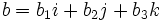
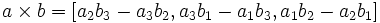
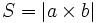
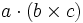
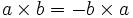
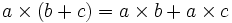
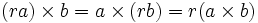
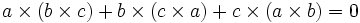
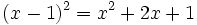
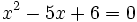

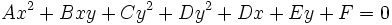
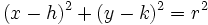
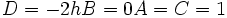
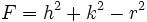

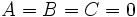
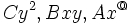
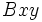
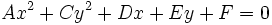
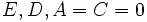
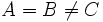
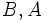
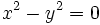
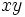
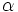
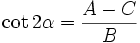
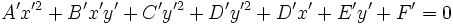
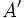
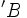
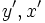
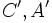

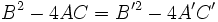
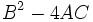
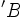
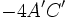
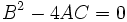
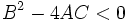
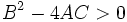
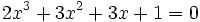
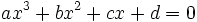
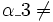
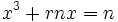
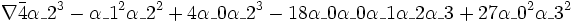
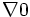
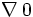
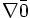
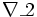
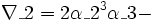
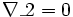
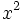
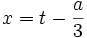
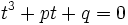
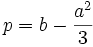
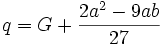
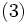
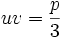
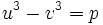
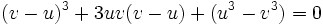
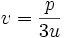
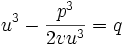
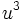
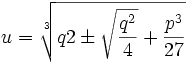
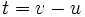
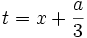
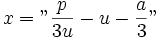
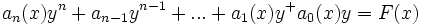
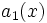
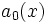
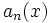
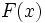
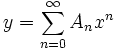
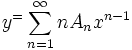
 حالت خطی
حالت خطی

