
|
|
|||||||
| مقالات و موضوعات علمی در این تالار مقالات و مطالب علمی قرار داده خواهد شد توجه شود که مقالات علمی و دانشگاهی با اخبار علمی تفاوت دارد و بخش مربوطه ی اخبار علمی به صورت جداگانه ایجاد شده است |
 |
|
|
ابزارهای موضوع | نحوه نمایش |
|
|
|
#1
|
||||
|
||||
|
مثلث قائمالزاویه مثلثی است که یکی از زوایای آن قائمه (۹۰ درجه) باشد
در حالت خاص اگر یکی از زوایا ۳۰ درجه باشد، ضلع مقابل آن زاویه نصف وتر است.وتر به ضلع روبرو به زاویه 90 درجه میگویند* بزرگترین ضلع در مثلث قائم الزاویه وتر است در مثلث قائمالزاویه مجموع مربعهای طول دو ضلع برابر با مربع طول وتر است. برابرنهاده فرهنگستان زبان فارسی دوره پیش از انقلاب برای واژه قائمالزاويه، «راستگوشه» بود که چندی هم در کتابهای درسی بکار رفت.
__________________
|
|
#2
|
||||
|
||||
|
3، 6، 10، 15، 21 و ... بنظر شما این اعداد چه ویژگی مشترکی دارند؟ اگر دست بهقلم نشویم و شکل نکشیم و آزمایش نکنیم، فهمیدن ارتباط میان آنها کمی دشوار است. بهاین شکل دقت کنید مشکل شما حل خواهد شد. به اعداد موجود در این سری، اعداد مثلثی میگوییم.
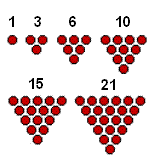 1 = 1 3= 1+2 6= 1+2+3 10= 1+2+3+4 15= 1+2+3+4+5 21= 1+2+3+4+5+6 . . . اما شکل اول یک ایده جدید به ما می دهد کهمی توانیم این اعداد را همانند پاراگراف بالا نیز تفسیر کنیم. به بیان دیگرمی توان گفت که هرعدد مثلثی تشکیل شده است از حاصل جمع یکسری از اعداد متوالیطبیعی. به این معنی که اولین عدد مثلثی مساوی است با مجموع یک عدد از اعداد طبيعي، دومین معادل است با مجموع دو عدد از اعداد طبیعی، سومین معادل است بامجموع سه عدد از اعداد طبیعی و ... و بالاخره n امین عدد مثلثی معادل است با مجموعn عدد از اعداد طبیعی که اگر رياضياتدبیرستان را هنوز فراموش نکرده باشید بخاطر خواهید آورد که مقدار این عدد معادلn(n+1)/2 خواهد بود. (یک تصاعد حسابيساده(  مجموع دو عدد مثلثی متوالی اگرهر دو عدد پشت سرهم در سری اعداد مثلثی را با هم جمع کنیم حاصل جمع یک عددمربعمی شود. مثلا" 1+3=4 یا 3+6=9 یا6+10=16 و ... البته دلیل آن ساده است به شکل دوم توجه کنید و ببینید که چگونه دو مثلثقرمز و سبز روی همتشکیل یک مربع را می دهند. (سعی کنید با استدلال ریاضی هم این موضوع را ثابت کنید،ساده است از همان رابطه بالا استفاده کنید.) مطلب اخیر اغلب بصورت قضیه مربع هر عدد طبیعی برابر است با مجموع دو عدد مثلثی متوالینیز مطرح می شود.
__________________
|
|
#3
|
||||
|
||||
|
شکلهای مسطح را هم نهشت گویند اگر همریخت و هم اندازه باشند. شکلهای همنهشت را میتوان با تبدیلی که نقاط را حرکت میدهد ، اما رابطه های برخوردی "incidence" (بین نقاط و خطوط)، زوایای بین خطوط، و طولهای پاره خطها را تغییر نمی دهد، بر هم منطبق کرد.
چنین تبدیلی سطحها را حفظ میکند و خطوط موازی را موازی جابجا میکند. اگر شکلهای همنهشت دارای جهت یکسان ( نسبت به جهت ثابتی از صفحه) باشند، آنها را میتوان با استفاده از دنباله ای از انتقالها و دوران های صفحه به هم تبدیل کرد. چنین شکلهایی را مستقیم-هم نهشت " directly congruent" می نامند. اگر دارای جهت یکسان نباشند آنگاه برای منطبق کردن یکی بر دیگری، میتوان دنباله ای را بدست آورد که غیر از انتقالها و دوران های متوالی حاوی تقارنی منفرد نسبت به خطی راست باشد. شکلهایی چنین را وارون - همنهشت "inversely congruent" می نامند. انتقالها ، دورانها و تقارنها به تبدیل های هم نهشتی موسوم اند و می توانند در بررسی شکلهای مسطح به عنوان معیارهای همنهشتی به کار روند، اما این کاربرد به هیچ وجه در برگیرنده سودمندی آنها به عنوان وسیله ای در کشف مطالب تازه هندسی نیست.
__________________
|
|
#4
|
||||
|
||||
|
چهار قضیه در مورد همنهشتی مثلثها
در تعریف همنهشتی نیاز است که شکلها در جمیع جنبه ها سازگار باشند، بخصوص طولهای اضلاع متناظر و زوایای بین انها برابر باشند. قضایای زیر بیان میکند که در مورد حالات خاصی از مثلثها کافی است که برای امتحان هم نهشتی سه جز آنها را مورد بررسی قرار دهیم. اگر این سه جز در دو مثلث برابر باشند مثلثها همنهشت هستند. چهار قضیه همنهشتی 1. دو مثلث هم نهشت اند اگر طول یک ضلع یکی از انها برابر طول ضلع نظیرش از دیگری و دو زاویه آنها برابر دو زاویه نظیرشان از دیگری باشد 2.دو مثلث هم نهشت اند اگر طولهای دو ضلع یکی برابر طولهای ضلعهای نظیرشان از دیگری و زاویه های بین این ضلعها برابر باشند 3.دو مثلث هم نهشت اند اگر طولهای دو ضلع یکی برابر طولهای ضلعهای نظیرشان از دیگری و زاویه های مقابل ضلع های بزرگتر آنها برابر باشند 4. دو مثلث هم نهشت اند اگر طولهای سه ضلع از یکی برابر طولهای ضلعهای نظیرشان از دیگری باشند. اشکال چهار قضیه 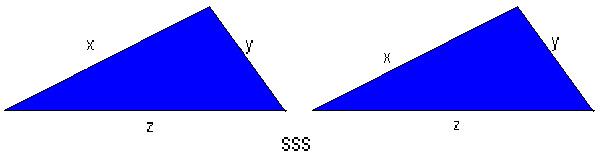  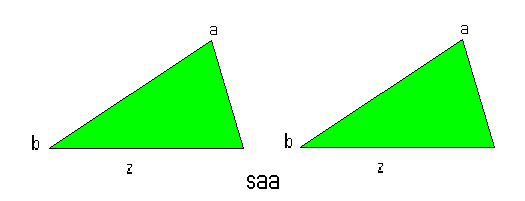 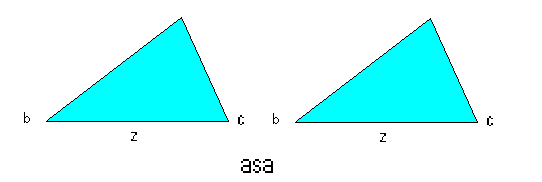
__________________
|
|
#5
|
||||
|
||||
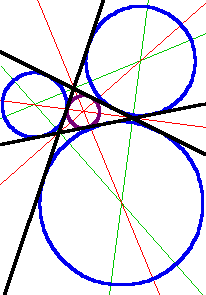 با دایره داخلی (بنفش)، دوایر خارجی (آبی)، نیمسازهای زوایای داخلی (قرمز) و نیمسازهای زوایای خارجی (سبز) دایره های محاطی داخلی و خارجی یک مثلث در هندسه، دایره محاطی داخلی یک مثلث بزرگترین دایرهای است که آن مثلث میتواند در بر بگیرد؛ این دایره سه ضلع آنرا لمس مینماید ( بر آنها مماس میباشد). مرکز دایره محاطی مرکز داخلی مثلث نامیده میشود. یک دایره محاطی خارجی مثلث، یک دایره در خارج مثلث است که بر یکی از اضلاع مثلث و امتداد دو ضلع دیگر مماس باشد. هر مثلث دارای سه دایره محاطی خارجی متمایز، که هر کدام بر یکی از اضلاع مثلث مماس میباشد. مرکز دایره محاطی داخلی بر روی تقاطع نیمسازهای زوایای داخلی قرار دارد. مرکز یک دایره محاطی خارجی بر روی تقاطع نیمساز یک زاویه داخلی و نیمسازهای خارجی دو زاویه دیگر قرار دارد. از این رو، استنباط میگردد که مرکز دایره محاطی داخلی و سه مرکز دایره های محاطی خارجی یک سیستم چهارمرکزی (orthocentric) را تشکیل میدهند. شعاع این دوایر ارتباط نزدیکی با سطح یک مثلث دارد. اگر S سطح مثلث و اضلاع آن b ،a و c باشند، شعاع دایره داخلی ( که "شعاع داخلی" نیز گفته میشود) برابر است با: (S/(2(a+b+c). شعاع دایره خارجی در سمت a برابر است با: (S/(2(-a+b+c)، برای دایره در سمت b برابر است با: (S/(2(a-b+c) و برای دایره در سمت c برابر است با: (S/(2(a+b-c). از این روابط درمیابیم که دوایر خارجی از دایره داخلی بزرگتراند و بزرگترین دایره خارجی، دایره ای است که به بزرگترین ضلع چسبیده است. Triangle with incircle, contact triangle and Gergonne pointمثلث با دایره داخلی (سیاه), مثلث تماس (قرمز)، نقطه جرگونه (سبز) دایره نه نقطه ای مثلث بر سه دایره خارجی و همچنین دایره داخلی مماس میباشد. نقطه فورباخ(Feuerbach) روی دایره داخلی قرار دارد. با علامت گذاری رئوس مثلث با B، A و C و سه نقطه تماس دایره داخلی و مثلث با TB، TA و TC (که TA روبروی A قرار داشته و به همین ترتیب بقیه)، مثلث TATBTC مثلث تماس ABC نامیده میشود. دایره داخلی ABC یک دایره محیطی بر TATBTC میباشد. سه خط BTB ، ATA و CTC در یک نقطه
__________________
|
 |
| کاربران در حال دیدن موضوع: 1 نفر (0 عضو و 1 مهمان) | |
|
|
اکنون ساعت 04:27 PM برپایه ساعت جهانی (GMT - گرینویچ) +3.5 می باشد.






 حالت ترکیبی
حالت ترکیبی
